Question

9．若二次函數(shù)y=ax²+bx+c的x與y的部分對應(yīng)值如下表：

x	…	-4	-3	-2	-1	0	…
y	…	-5	0	3	4	3	…

（1）求此二次函數(shù)的解析式；
（2）畫出此函數(shù)圖象（不用列表）．
（3）結(jié)合函數(shù)圖象，當(dāng)-4＜x≤1時，寫出y的取值范圍．

Answer 1

分析 （1）利用表中數(shù)據(jù)和拋物線的對稱性可得到拋物線的頂點坐標(biāo)為（-1，4），則可設(shè)頂點式y(tǒng)=a（x+1）²+4，然后把（0，3）代入求出a的值即；
（2）利用描點法畫二次函數(shù)圖象；
（3）觀察函數(shù)函數(shù)圖象，當(dāng)-4＜x≤1時，函數(shù)的最大值為4，于是可得到y(tǒng)的取值范圍為-5＜y≤4．

解答 解：（1）由表知，拋物線的頂點坐標(biāo)為（-1，4），設(shè)y=a（x+1）²+4，
把（0，3）代入得a（0+1）²+4=3，解得a=-1，
∴拋物線的解析式為y=-（x+1）²+4，即y=-x²-2x+3；
（2）如圖，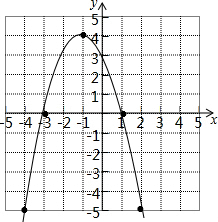

（3）當(dāng)-4＜x≤1時，-5＜y≤4．

點評 本題考查了待定系數(shù)法求二次函數(shù)的解析式：在利用待定系數(shù)法求二次函數(shù)關(guān)系式時，要根據(jù)題目給定的條件，選擇恰當(dāng)?shù)姆椒ㄔO(shè)出關(guān)系式，從而代入數(shù)值求解．一般地，當(dāng)已知拋物線上三點時，常選擇一般式，用待定系數(shù)法列三元一次方程組來求解；當(dāng)已知拋物線的頂點或?qū)ΨQ軸時，常設(shè)其解析式為頂點式來求解；當(dāng)已知拋物線與x軸有兩個交點時，可選擇設(shè)其解析式為交點式來求解．也考查了二次函數(shù)的性質(zhì)．