Question

19．將下列推理過程填寫完整．
（1）如圖1，已知∠B+∠BED+∠D=360°，求證AB∥CD．
證明：過E點(diǎn)作EF∥CD（過直線外一點(diǎn)有且只有一條直線與已知直線平行）
∵EF∥CD，
∴∠D+∠DEF=180°，（兩直線平行，同旁內(nèi)角互補(bǔ)）
∵∠B+∠BED+∠D=360°，（已知）
∴∠B+∠BEF=∠B+∠BED+∠D-（∠D+∠DEF）=360°-180°=180°
∴EF∥AB，（同旁內(nèi)角互補(bǔ)，兩直線平行）
∴AB∥CD，（平行于同一直線的兩直線平行）
（2）如圖2，已知∠BED=∠B+∠D，求證AB∥CD．
證明：過E點(diǎn)作EF∥CD（過直線外一點(diǎn)有且只有一條直線與已知直線平行）
∵EF∥CD，
∴∠D=∠FED，（兩直線平行，內(nèi)錯(cuò)角相等）
∵∠BED=∠B+∠D（已知）
∴∠B=∠BEF-∠D=∠BED-∠FED=∠BEF，
∴AB∥EF，（內(nèi)錯(cuò)角相等，兩直線平行）
∴AB∥CD．（平行于同一直線的兩直線平行）

Answer 1

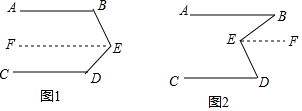
分析 （1）過E點(diǎn)作EF∥CD，首先根據(jù)平行線的性質(zhì)可得∠D+∠DEF=180°，然后可得∠B+∠BEF=180°，進(jìn)而可根據(jù)同旁內(nèi)角互補(bǔ)，兩直線平行可得AB∥CD；
（2）過E點(diǎn)作EF∥CD，根據(jù)平行線的性質(zhì)可得∠D=∠FED，進(jìn)而可得∠B=∠BEF，根據(jù)內(nèi)錯(cuò)角相等，兩直線平行可得AB∥EF，再根據(jù)平行于同一直線的兩直線平行可得AB∥CD．

解答 （1）證明：過E點(diǎn)作EF∥CD（過直線外一點(diǎn)有且只有一條直線與已知直線平行）
∵EF∥CD，
∴∠D+∠DEF=180°，（  兩直線平行，同旁內(nèi)角互補(bǔ) ）
∵∠B+∠BED+∠D=360°，（ 已知 ）
∴∠B+∠BEF=∠B+∠BED+∠D-（∠D+∠DEF ）=360°-180°=180°，
∴EF∥AB，（ 同旁內(nèi)角互補(bǔ)，兩直線平行 ） 
∴AB∥CD，（  平行于同一直線的兩直線平行）；
故答案為：兩直線平行，同旁內(nèi)角互補(bǔ)；同旁內(nèi)角互補(bǔ)，兩直線平行；AB；CD；

（2）證明：過E點(diǎn)作EF∥CD（過直線外一點(diǎn)有且只有一條直線與已知直線平行）
∵EF∥CD，
∴∠D=∠FED，（ 兩直線平行，內(nèi)錯(cuò)角相等 ）
∵∠BED=∠B+∠D，（已知）
∴∠B=∠BED-∠D=∠BED-∠FED=∠BEF，
∴AB∥EF，（ 內(nèi)錯(cuò)角相等，兩直線平行 ） 
∴AB∥CD，（  平行于同一直線的兩直線平行）．
故答案為：兩直線平行，內(nèi)錯(cuò)角相等；AB；EF；內(nèi)錯(cuò)角相等，兩直線平行；AB；CD．

點(diǎn)評 此題主要考查了平行線的判定和性質(zhì)，關(guān)鍵是掌握兩直線平行，內(nèi)錯(cuò)角相等，同旁內(nèi)角互補(bǔ)；內(nèi)錯(cuò)角相等或同旁內(nèi)角互補(bǔ)，兩直線平行．