
分析 根據實數運算的法則,以及分式運算的法則即可求出答案.
解答 解:(1)原式=2-1+3
=4
(2)原式=$\frac{{a{b^2}}}{{2{c^2}}}÷\frac{{3{a^2}{b^2}}}{4cd}•\frac{9}{{4{d^2}}}$
=$\frac{{a{b^2}}}{{2{c^2}}}•\frac{4cd}{{3{a^2}{b^2}}}•\frac{9}{{4{d^2}}}$
=$\frac{{a{b^2}}}{{2{c^2}}}•\frac{4cd}{{3{a^2}{b^2}}}•\frac{9}{{4{d^2}}}$
=$\frac{3}{2acd}$
點評 本題考查學生的運算能力,涉及實數混合運算,分式混合運算,本題屬于基礎題型.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
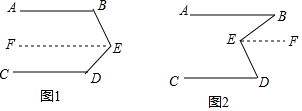 將下列推理過程填寫完整.
將下列推理過程填寫完整.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
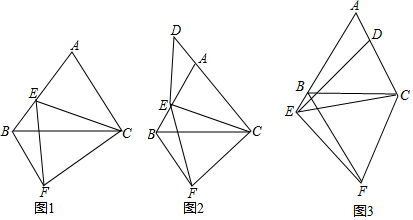
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增減 | +5 | -2 | -4 | +12 | -10 | +16 | -9 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知數軸上有A、B、C三個點,它們表示的數分別是a、b和8,O是原點,且(a+20)2+|b+10|=0.
如圖,已知數軸上有A、B、C三個點,它們表示的數分別是a、b和8,O是原點,且(a+20)2+|b+10|=0.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com