
2.已知向量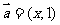 ,
,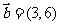 ,且
,且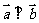 ,則實數(shù)
,則實數(shù)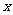 的值為( )
的值為( )
A.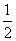 B.
B.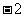 C.
C.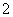 D.
D.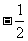
1.若集合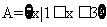 ,
,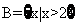 ,則
,則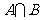 等于( )
等于( )
A.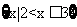 B.
B.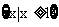 C.
C.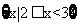 D.
D.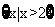
3. 3.用 x,
x, y,
y, z,
z, (x+y),
(x+y), (x-y)表示下列各式:
(x-y)表示下列各式:
(1) 
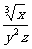 ;
(2)
;
(2) (
(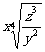 );
);
(3)  (
(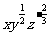 ); (4)
); (4)
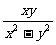 ;
;
(5) (
(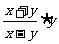 ); (6)
); (6) [
[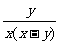 ]3.
]3.
解:(1) 
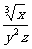 =
=
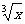 -
-
 z
z
=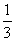
 x-(2
x-(2 y+
y+ z)
z)
=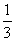
 x-2
x-2 y-
y- z;
z;
(2)  (x·
(x·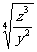 )=
)= x+
x+
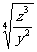
= x+
x+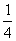 (
(
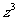 -
-
 )
)
= x-
x-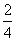
 y+
y+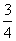
 z
z
= x-
x- y+
y+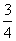
 z;
z;
(3)  (x
(x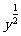
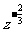 )=
)= x+
x+
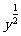 +
+
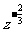 ?
?
= x+
x+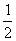
 y-
y-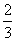
 z;
z;
(4) 
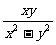 =
= xy-
xy- (
(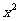 -
- )
)
= x+
x+ y-
y- (x+y)(x-y)
(x+y)(x-y)
= x+
x+ y-
y- (x+y)-
(x+y)- (x-y);
(x-y);
(5)  (
(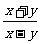 ·y)=
·y)=
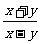 +
+ y
y
= (x+y)-
(x+y)- (x-y)+
(x-y)+ y;
y;
(6)  [
[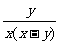 ]
]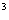
=3[ y-
y- x-
x- (x-y)]
(x-y)]
=3 y-3
y-3 x-3
x-3 (x-y)
(x-y)
2.已知lg2=0.3010,lg3=0.4771,求下列各對數(shù)的值(精確到小數(shù)點后第四位)
(1) lg6 (2)lg4 (3)lg12
(4)lg 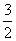 (5)lg
(5)lg 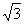 (6)lg32
(6)lg32
解:(1)lg6=lg2+lg3=0.3010+0.4771=0.7781
(2) lg4=2lg2=2×0.3010=0.6020
(3) lg12=lg(3×4)=lg3+2lg2=0.4771+0.3010×2=1.0791
(4) lg 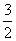 =lg3-lg2=0.4771-0.3010=0.1761
=lg3-lg2=0.4771-0.3010=0.1761
(5) lg 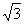 =
=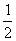 lg3=
lg3=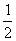 ×0.4771=0.2386
×0.4771=0.2386
(6) lg32=5lg2=5×0.3010=1.5050
1.計算:
(1)  2+
2+
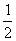 (a>0,a≠1) (2)
(a>0,a≠1) (2) 18-
18- 2
2
(3) lg 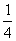 -lg25
(4)2
-lg25
(4)2 10+
10+ 0.25
0.25
(5)2 25+3
25+3 64
(6)
64
(6)  (
( 16)
16)
解:(1)  2+
2+
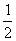 =
= (2×
(2×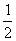 )=
)= 1=0
1=0
(2)  18-
18- 2=
2=
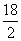 =
= 9=2
9=2
(3)lg 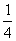 -lg25=lg(
-lg25=lg(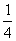 ÷25)=lg
÷25)=lg 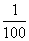 =lg
=lg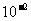 =-2
=-2
(4)2 10+
10+ 0.25=
0.25=
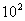 +
+ 0.25
0.25
= (100×0.25)=
(100×0.25)= 25=2
25=2
(5)2 25+3
25+3 64=2
64=2
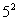 +3
+3
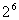
=2×2+3×6=22
(6)  (
( 16)=
16)= (
(
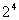 )=
)= 4=
4=
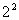 =2
=2
2. 用lgx,lgy,lgz表示下列各式:
(1) lg(xyz); (2)lg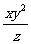 ; (3)
; (3)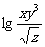 ; (4)
; (4)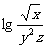
解:(1) lg(xyz)=lgx+lgy+lgz;
(2) lg 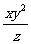 =lgx
=lgx -lgz=lgx+lg
-lgz=lgx+lg -lgz
-lgz
=lgx+2lgy-lgz;
(3) 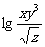 =lgx
=lgx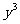 -lg
-lg 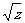 =lgx+lg
=lgx+lg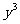 -
-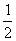 lgz
lgz
=lgx+3lgy-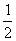 lgz;
lgz;
(4)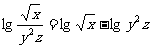
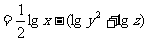

1.求下列各式的值:
(1) 6-
6- 3
3 (2)lg5+lg2
(2)lg5+lg2
(3) 3+
3+
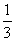
 (4)
(4) 5-
5- 15
15
解:(1) 6-
6- 3=
3=
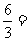
 2=1
2=1
(2)lg5+lg2=lg(5×2)=lg10=1
(3)  3+
3+
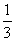 =
= (3×
(3×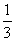 )=
)= 1=0
1=0
(4)  5-
5- 15=
15=
 =
=
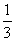 =-
=- 3=-1.
3=-1.
例1 計算
(1) 25, (2)
25, (2)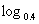 1, (3)
1, (3) (
(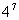 ×
×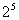 ), (4)lg
), (4)lg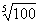
解:(1) 25=
25= 
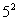 =2
=2
(2)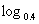 1=0
1=0
(3) (
(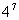 ×25)=
×25)= 
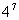 +
+ 
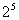
= 
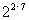 +
+ 
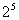 = 2×7+5=19
= 2×7+5=19
(4)lg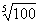 =
=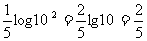

例2 用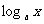 ,
,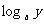 ,
,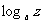 表示下列各式:
表示下列各式:


解:(1) =
= (xy)-
(xy)- z=
z= x+
x+ y-
y-  z
z
(2)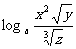 =
= (
(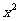
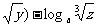
= 
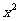 +
+
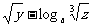 =2
=2 x+
x+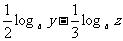

例3計算:
(1)lg14-2lg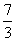 +lg7-lg18
(2)
+lg7-lg18
(2)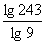 (3)
(3)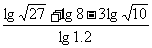
說明:此例題可講練結(jié)合.
(1)解法一:lg14-2lg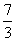 +lg7-lg18
+lg7-lg18
=lg(2×7)-2(lg7-lg3)+lg7-lg(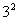 ×2)
×2)
=lg2+lg7-2lg7+2lg3+lg7-2lg3-lg2=0 ?
?
解法二:
lg14-2lg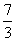 +lg7-lg18=lg14-lg
+lg7-lg18=lg14-lg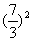 +lg7-lg18?
+lg7-lg18?
=lg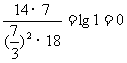

評述:此題體現(xiàn)了對數(shù)運算性質(zhì)的靈活運用,運算性質(zhì)的逆用常被學生所忽視.
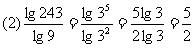

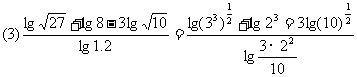

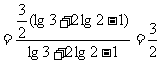

評述:此例題體現(xiàn)對數(shù)運算性質(zhì)的綜合運用,應注意掌握變形技巧,如(3)題各部分變形要化到最簡形式,同時注意分子、分母的聯(lián)系.(2)題要避免錯用對數(shù)運算性質(zhì).
積、商、冪的對數(shù)運算法則:
如果 a > 0,a ¹ 1,M > 0, N > 0 有:
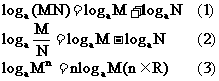
證明:①設(shè)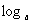 M=p,
M=p,  N=q
N=q
由對數(shù)的定義可以得:M=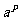 ,N=
,N=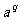

∴MN= 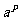
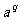 =
=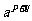 ∴
∴ MN=p+q,
MN=p+q,
即證得 MN=
MN= M +
M +  N
N
②設(shè) M=p,
M=p, N=q
N=q
由對數(shù)的定義可以得M=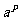 ,N=
,N=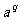

∴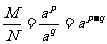 ∴
∴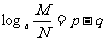

即證得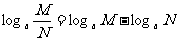

③設(shè) M=P 由對數(shù)定義可以得M=
M=P 由對數(shù)定義可以得M=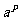 ,
,
∴ =
=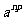 ∴
∴
 =np, 即證得
=np, 即證得
 =n
=n M
M
說明:上述證明是運用轉(zhuǎn)化的思想,先通過假設(shè),將對數(shù)式化成指數(shù)式,并利用冪的運算性質(zhì)進行恒等變形;然后再根據(jù)對數(shù)定義將指數(shù)式化成對數(shù)式
①簡易語言表達:“積的對數(shù) = 對數(shù)的和”……
②有時逆向運用公式:如

③真數(shù)的取值范圍必須是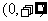 :
:
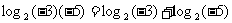 是不成立的
是不成立的
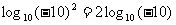 是不成立的
是不成立的
④對公式容易錯誤記憶,要特別注意:
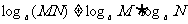 ,
,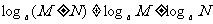

3.指數(shù)運算法則 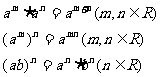

湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com