日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

2．機械波的分類

機械波可分為橫波和縱波兩種。

(1)質點振動方向和波的傳播方向垂直的叫橫波，如：繩上波、水面波等。

(2)質點振動方向和波的傳播方向平行的叫縱波，如：彈簧上的疏密波、聲波等。

說明：地震波既有橫波，也有縱波。

1．機械波的產生條件：①波源(機械振動)②傳播振動的介質(相鄰質點間存在相互作用力)。

2．共振

當驅動力的頻率跟物體的固有頻率相等時，受迫振動的振幅最大，這種現象叫共振。

要求會用共振解釋現象，知道什么情況下要利用共振，什么情況下要防止共振。

(1)利用共振的有：共振篩、轉速計、微波爐、打夯機、跳板跳水、打秋千……

(2)防止共振的有：機床底座、航海、軍隊過橋、高層建筑、火車車廂……

[例11] 把一個篩子用四根彈簧支起來，篩子上裝一個電動偏心輪，它每轉一周，給篩子一個驅動力，這就做成了一個共振篩。不開電動機讓這個篩子自由振動時，完成20次全振動用15s；在某電壓下，電動偏心輪的轉速是88r/min。已知增大電動偏心輪的電壓可以使其轉速提高，而增加篩子的總質量可以增大篩子的固有周期。為使共振篩的振幅增大，以下做法正確的是

A．降低輸入電壓　　　　　　　 B．提高輸入電壓

C．增加篩子質量　 　　　　　　D．減小篩子質量

解析：篩子的固有頻率為f_固=4/3Hz，而當時的驅動力頻率為f_驅=88/60Hz，即f_固< f_驅。為了達到振幅增大，應該減小這兩個頻率差，所以應該增大固有頻率或減小驅動力頻率。本題應選AD。

[例12]　 一物體做受迫振動，驅動力的頻率小于該物體的固有頻率。當驅動力的頻率逐漸增大時，該物體的振幅將：( )

A．逐漸增大

B．先逐漸減小后逐漸增大；　

C．逐漸減小

D．先逐漸增大后逐漸減小

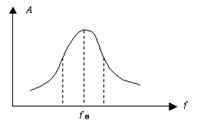
解析：此題可以由受迫振動的共振曲線圖來判斷。

受迫振動中物體振幅的大小和驅動力頻率與系統固有頻率之差有關。驅動力的頻率越接近系統的固有頻率，驅動力與固有頻率的差值越小，作受迫振動的振子的振幅就越大。當外加驅動力頻率等于系統固有頻率時，振動物體發生共振，振幅最大。　 由共振曲線可以看出，當驅動力的頻率小于該物體的固有頻率時，增大驅動力頻率，振幅增大，直到驅動力頻率等于系統固有頻率時，振動物體發生共振，振幅最大。在此之后若再增大驅動力頻率，則振動物體的振幅減小。

所以本題的正確答案為D。

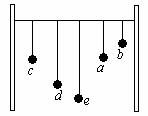
[例13]如圖所示，在一根張緊的水平繩上，懸掛有 a、b、c、d、e五個單擺，讓a擺略偏離平衡位置后無初速釋放，在垂直紙面的平面內振動；接著其余各擺也開始振動。下列說法中正確的有：( )

A．各擺的振動周期與a擺相同

B．各擺的振幅大小不同，c擺的振幅最大

C．各擺的振動周期不同，c擺的周期最長

D．各擺均做自由振動

解析：a擺做的是自由振動，周期就等于a擺的固有周期，其余各擺均做受迫振動，所以振動周期均與a擺相同。 　c擺與a擺的擺長相同，所以c擺所受驅動力的頻率與其固有頻率相等，這樣c擺產生共振，故c擺的振幅最大。

此題正確答案為A、B。

1．受迫振動

物體在驅動力(既周期性外力)作用下的振動叫受迫振動。

⑴物體做受迫振動的頻率等于驅動力的頻率，與物體的固有頻率無關。

⑵物體做受迫振動的振幅由驅動力頻率和物體的固有頻率共同決定：兩者越接近，受迫振動的振幅越大，兩者相差越大受迫振動的振幅越小。

3．圖象的用途：從圖象中可以知道：

(1)任一個時刻質點的位移　　 (2)振幅A．　 (3)周期T

(4)速度方向：由圖線隨時間的延伸就可以直接看出

(5)加速度：加速度與位移的大小成正比，而方向總與位移方向相反．只要從振動圖象中認清位移(大小和方向)隨時間變化的規律，加速度隨時間變化的情況就迎刃而解了

點評：關于振動圖象的討論

(1)簡諧運動的圖象不是振動質點的軌跡．做簡諧運動質點的軌跡是質點往復運動的那一段線段(如彈簧振子)或那一段圓弧(如下一節的單擺)．這種往復運動的位移圖象。就是以x軸上縱坐標的數值表示質點對平衡位置的位移。以t軸橫坐標數值表示各個時刻，這樣在x-t坐標系內，可以找到各個時刻對應質點位移坐標的點，即位移隨時間分布的情況--振動圖象．

(2)簡諧運動的周期性，體現在振動圖象上是曲線的重復性． 簡諧運動是一種復雜的非勻變速運動．但運動的特點具有簡單的周期性、重復性、對稱性．所以用圖象研究要比用方程要直觀、簡便．簡諧運動的圖象隨時間的增加將逐漸延伸，過去時刻的圖形將永遠不變，任一時刻圖線上過該點切線的斜率數值代表該時刻振子的速度大小。正負表示速度的方向，正時沿x正向，負時沿x負向．

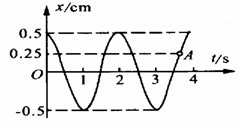
[例9]　 勁度系數為20N／cm的彈簧振子，它的振動圖象如圖所示，在圖中A點對應的時刻

A． 振子所受的彈力大小為0．5N，方向指向x軸的負方向

B．振子的速度方向指向x軸的正方向

C． 在0-4s內振子作了1．75次全振動

D。在0-4s內振子通過的路程為0．35cm，位移為0

解析：由圖可知A在t軸上方，位移x＝0．25cm，所以彈力F＝－kx＝－5N，即彈力大小為5N，方向指向x軸負方向，選項A不正確；由圖可知過A點作圖線的切線，該切線與x軸的正方向的夾角小于90°，切線斜率為正值，即振子的速度方向指向x軸的正方向，選項B正確．　 由圖可看出，t＝0、t＝4s時刻振子的位移都是最大，且都在t軸的上方，在0-4s內完成兩次全振動，選項C錯誤．由于t＝0時刻和t＝4s時刻振子都在最大位移處，所以在0-4s內振子的位移為零，又由于振幅為0．5cm，在0-4s內振子完成了2次全振動，所以在這段時間內振子通過的路程為2×4×0．50cm＝4cm，故選項D錯誤．

綜上所述，該題的正確選項為B．

[例10]　 擺長為L的單擺做簡諧振動，若從某時刻開始計時，(取作t=0)，當振動至 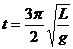時，擺球具有負向最大速度，則單擺的振動圖象是圖中的(　 )　

　解析：從t=0時經過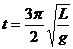時間，這段時間為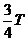，經過 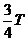擺球具有負向最大速度，說明擺球在平衡位置，在給出的四個圖象中，經過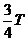具有最大速度的有C、D兩圖，而具有負向最大速度的只有D。所以選項D正確。

2．振動圖象的含義：振動圖象表示了振動物體的位移隨時間變化的規律．

1．簡諧運動的圖象：以橫軸表示時間t，以縱軸表示位移x，建立坐標系，畫出的簡諧運動的位移--時間圖象都是正弦或余弦曲線．

2．單擺。

(1)單擺振動的回復力是重力的切向分力，不能說成是重力和拉力的合力。在平衡位置振子所受回復力是零，但合力是向心力，指向懸點，不為零。

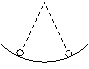(2)當單擺的擺角很小時(小于5°)時，單擺的周期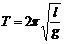，與擺球質量m、振幅A都無關。其中l為擺長，表示從懸點到擺球質心的距離，要區分擺長和擺線長。

(3)小球在光滑圓弧上的往復滾動，和單擺完全等同。只要擺角足夠小，這個振動就是簡諧運動。這時周期公式中的l應該是圓弧半徑R和小球半徑r的差。

(4)擺鐘問題。單擺的一個重要應用就是利用單擺振動的等時性制成擺鐘。在計算擺鐘類的問題時，利用以下方法比較簡單：在一定時間內，擺鐘走過的格子數n與頻率f成正比(n可以是分鐘數，也可以是秒數、小時數……)，再由頻率公式可以得到：

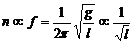
[例6] 已知單擺擺長為L，懸點正下方3L/4處有一個釘子。讓擺球做小角度擺動，其周期將是多大？

解析：該擺在通過懸點的豎直線兩邊的運動都可以看作簡諧運動，周期分別為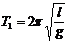和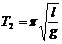，因此該擺的周期為 ：

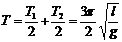
[例7] 固定圓弧軌道弧AB所含度數小于5°，末端切線水平。兩個相同的小球a、b分別從軌道的頂端和正中由靜止開始下滑，比較它們到達軌道底端所用的時間和動能：t_a＿＿t_b，E_a＿＿2E_b。

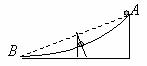
解析：兩小球的運動都可看作簡諧運動的一部分，時間都等于四分之一周期，而周期與振幅無關，所以t_a= t_b；從圖中可以看出b小球的下落高度小于a小球下落高度的一半，所以E_a>2E_b。

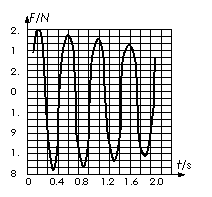
[例8] 將一個力電傳感器接到計算機上，可以測量快速變化的力。用這種方法測得的某單擺擺動過程中懸線上拉力大小隨時間變化的曲線如右圖所示。由此圖線提供的信息做出下列判斷：①t＝0．2s時刻擺球正經過最低點；②t＝1．1s時擺球正處于最高點；③擺球擺動過程中機械能時而增大時而減小；④擺球擺動的周期約是T＝0．6s。上述判斷中正確的是　 　　　

A．①③　　 B．②④　 　 C．①②　　 D．③④

解析：注意這是懸線上的拉力圖象，而不是振動圖象。當擺球到達最高點時，懸線上的拉力最小；當擺球到達最低點時，懸線上的拉力最大。因此①②正確。從圖象中看出擺球到達最低點時的拉力一次比一次小，說明速率一次比一次小，反映出振動過程擺球一定受到阻力作用，因此機械能應該一直減小。在一個周期內，擺球應該經過兩次最高點，兩次最低點，因此周期應該約是T＝1．2s。因此答案③④錯誤。本題應選C。

1．彈簧振子

(1)周期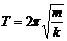，與振幅無關，只由振子質量和彈簧的勁度決定。

(2)可以證明，豎直放置的彈簧振子的振動也是簡諧運動，周期公式也是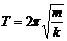。這個結論可以直接使用。

(3)在水平方向上振動的彈簧振子的回復力是彈簧的彈力；在豎直方向上振動的彈簧振子的回復力是彈簧彈力和重力的合力。

[例1] 有一彈簧振子做簡諧運動，則　 (　　 )

A．加速度最大時，速度最大　 B．速度最大時，位移最大

C．位移最大時，回復力最大　 D．回復力最大時，加速度最大

解析：振子加速度最大時，處在最大位移處，此時振子的速度為零，由F= - kx知道，此時振子所受回復力最大，所以選項A錯，C、D對．振子速度最大時，是經過平衡位置時，此時位移為零，所以選項B錯．故正確選項為C、D

點評：分析振動過程中各物理量如何變化時，一定要以位移為橋梁理清各物理量間的關系：位移增大時，回復力、加速度、勢能均增大，速度、動量、動能均減小；位移減小時，回復力、加速度、勢能均減小，速度、動量、動能均增大．各矢量均在其值為零時改變方向，如速度、動量均在最大位移處改變方向，位移、回復力、加速度均在平衡位置改變方向．

[例2]　 試證明豎直方向的彈簧振子的振動是簡諧運動．

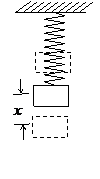解析：如圖所示，設振子的平衡位置為O，向下方向為正方向，此時彈簧的形變為 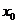，根據胡克定律及平衡條件有

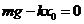　　 ①

當振子向下偏離平衡位置為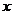時，回復力(即合外力)為

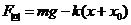　　 ②

將①代人②得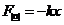：，可見，重物振動時的受力符合簡諧運動的條件．

點評：(1)分析一個振動是否為簡諧運動，關鍵是判斷它的回復力是否滿足其大小與位移成正比，方向總與位移方向相反．證明思路為：確定物體靜止時的位置--即為平衡位置，考查振動物體在任一點受到回復力的特點是否滿足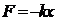。(2)還要知道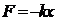中的k是個比例系數，是由振動系統本身決定的，不僅僅是指彈簧的勁度系數．關于這點，在這里應理解為是簡諧運動回復力的定義式．而且產生簡諧運動的回復力可以是一個力，也可以是某個力的分力或幾個力的合力．此題中的回復力為彈力和重力的合力．

[例3] 如圖所示，質量為m的小球放在勁度為k的輕彈簧上，使小球上下振動而又始終未脫離彈簧。(1)最大振幅A是多大？(2)在這個振幅下彈簧對小球的最大彈力F_m是多大？

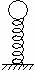
解析：該振動的回復力是彈簧彈力和重力的合力。在平衡位置彈力和重力等大反向，合力為零；在平衡位置以下，彈力大于重力，F- mg=ma，越往下彈力越大；在平衡位置以上，彈力小于重力，mg-F=ma，越往上彈力越小。平衡位置和振動的振幅大小無關。因此振幅越大，在最高點處小球所受的彈力越小。極端情況是在最高點處小球剛好未離開彈簧，彈力為零，合力就是重力。這時彈簧恰好為原長。

(1)最大振幅應滿足kA=mg，　 A=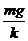

(2)小球在最高點和最低點所受回復力大小相同，所以有：F_m-mg=mg，F_m=2mg

[例4]彈簧振子以O點為平衡位置在B、C兩點之間做簡諧運動．B、C相距20 cm．某時刻振子處于B點．經過0.5 s，振子首次到達C點．求：

(1)振動的周期和頻率；

(2)振子在5 s內通過的路程及位移大小；

(3)振子在B點的加速度大小跟它距O點4 cm處P點的加速度大小的比值．

解析：(1)設振幅為A，由題意BC＝2A＝10 cm，所以A＝10 cm．振子從B到C所用時間t＝0．5s．為周期T的一半，所以T＝1．0s；f＝1/T＝1．0Hz．

(2)振子在1個周期內通過的路程為4A。故在t＝5s＝5T內通過的路程s＝t/T×4A＝200cm．5 s內振子振動了5個周期，5s末振子仍處在B點，所以它偏離平衡位置的位移大小為10cm．

(3)振子加速度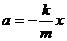．a∝x，所以a_B：a_P＝x_B：x_p＝10：4＝5：2．

[例5]一彈簧振子做簡諧運動．周期為T

A．若t時刻和(t+△t)時刻振子運動速度的大小相等、方向相反，則Δt一定等于T/2的整數倍

D．若t時刻和(t+△t)時刻振子運動位移的大小相等、方向相同，則△t一定等于T的整數倍

C．若△t＝T／2，則在t時刻和(t－△t)時刻彈簧的長度一定相等

D．若△t＝T，則在t時刻和(t－△t)時刻振子運動的加速度一定相同

解析：若△t＝T／2或△t＝nT－T/2，(n＝1，2，3．．．．)，則在t 和(t+△t)兩時刻振子必在關于干衡位置對稱的兩位置(包括平衡位置)，這兩時刻．振子的位移、回復力、加速度、速度等均大小相等，方向相反．但在這兩時刻彈簧的長度并不一定相等(只有當振子在t和(t－△t)兩時刻均在平衡位置時，彈簧長度才相等)．反過來．若在t和(t－△t)，兩時刻振子的位移(回復力、加速度)和速度(動量)均大小相等．方向相反，則△t一定等于△t＝T／2的奇數倍．即△t＝(2n－1)T/2(n＝1，2，3…)．如果僅僅是振子的速度在t 和(t+△t)，兩時刻大小相等方向相反，那么不能得出△t＝(2n一1)T/2，更不能得出△t＝nT/2(n＝1，2，3…)．根據以上分析．A、C選項均錯．

若t和(t+△t)時刻，振子的位移(回復力、加速度)、速度(動量)等均相同，則△t＝nT(n＝1，2，，3…)，但僅僅根據兩時刻振子的位移相同，不能得出△t＝nT．所以B這項錯．若△t＝T，在t和(t+△t)兩時刻，振子的位移、回復力、加速度、速度等均大　 小相等方向相同，D選項正確。

3．從總體上描述簡諧運動的物理量

振動的最大特點是往復性或者說是周期性。因此振動物體在空間的運動有一定的范圍，用振幅A來描述；在時間上則用周期T來描述完成一次全振動所須的時間。

(1)振幅A是描述振動強弱的物理量。(一定要將振幅跟位移相區別，在簡諧運動的振動過程中，振幅是不變的而位移是時刻在改變的)

(2)周期T是描述振動快慢的物理量。(頻率f=1/T 也是描述振動快慢的物理量)周期由振動系統本身的因素決定，叫固有周期。任何簡諧運動都有共同的周期公式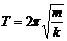：(其中m是振動物體的質量，k是回復力系數，即簡諧運動的判定式F= -kx中的比例系數，對于彈簧振子k就是彈簧的勁度，對其它簡諧運動它就不再是彈簧的勁度了)。