
4.下列各句中加點成語使用恰當的一項 ( )

A. 李春曉老師熱愛教育事業,幾十年如一日,好為人師,為國家培養了大批英才。
B. 我覺得,在快節奏的現代化生活里,這種與熒屏相映成趣的電視化小說也許會大行其道。
C. 這些年輕的登山運動員決心以無所不為的勇氣,克服重重困難,去征服珠穆朗瑪峰。
D. 美國政府在臺灣問題上的危言危行,只能搬起石頭砸自己的腳。
3.下列各句中沒有語病且句意明確的一句是( )
A.大家都有這樣的經驗,早晨腦子是最清醒的時候。
B.有些作品之所以屢屢出現錯誤,是因為作者思想水平低和文字功夫差等原因造成的。
C.我市藥品食品監督部門已著手按照誠信度等級對全市食品生產企業進行分類管理,不良記錄的多少,將直接影響企業的誠信等級
D.在當今這個競爭異常激烈的時代,任何一個企業家都不可能永遠經歷著輝煌而不面對挫折;遇到挫折并不可怕,可怕的是能否從失敗的陰影中走出來。
2.下列各句橫線處應填入的詞句,最恰當的一組是( )
① 幾年未見,那個頭發亂蓮蓬、小臉臟兮兮的外甥女嬌嬌,已經 得白白凈凈、亭亭玉立了,雖依舊親熱,但矜持了許多。
② 學生手中的課外讀物五花八門,有的書籍內容和插圖甚至低俗得讓人
,這樣的書籍對青少年的身心健康危害極大。
③ “3.19”大案發生后,專案組在圈定的幾個嫌疑人被相繼排除之后,只好采取大規模的摸排行動。經過半個月的排查,案情仍無進展。“
,
”正當案情陷入困境時,傳來好消息:摸排人員發現了一條極其重要的線索。
A.出落 不堪入目 山重水復疑無路,柳暗花明又一村
B.保養 不忍卒讀 山重水復疑無路,柳暗花明又一村
C.保養 不堪入目 踏破鐵鞋無覓處,得來全不費功夫
D.出落 不忍卒讀 踏破鐵鞋無覓處,得來全不費功夫
1.下列各項中加點字的讀音和書寫全都正確的一項是( ) 
A.痙(jīng)攣 涇(jīng)渭分明 睚眥(cī)必報 愴(chuàng)然淚下
B.峻(jùn)工 不瘟(wēn)不火 鍥(qiè)而不舍 怙惡不悛(quān)
C.癖(pǐ)好 諄(zhūn)諄告誡 淋漓盡至(zhì) 弱不禁(jīn)風
D.駭(hài)異 一抔(póu)黃土 矯揉(róu)造作 頭暈目眩(xuàn)
(五)用遞推方法解題
11、(03年全國)設{an}是首項為1的正項數列,且(n+1)a2n+1-nan2+an+1an=0,求它的通項公式是__1/n
12、(04年全國)已知數列{an}滿足a.1=1,an=a1+2a2+3a3+---+(n-1)an-1
(n>1),則{an}的通項an=______a1=1;an= n
n 2
2
13、(04年北京)定義“等和數列”:在一個數列中,如果每一項與它的后一項的和都為同一個常數,那么這個數列叫做等和數列,這個常數叫做該數列的公和。
已知數列是等和數列,且,公和為5,那么的值為__3___,這個數列的前n項和的計算公式為__當n為偶數時,;當n為奇數時,
14. (04年全國)已知數列{an}中,a1=1,a2k=a2k-1+(-1)K,a2k+1=a2k+3k,其中k=1,2,3,…。
(1)求a3,a5; (2)求{an}的通項公式
解:(I)a2=a1+(-1)1=0, a3=a2+31=3.a4=a3+(-1)2=4 a5=a4+32=13, 所以,a3=3,a5=13.
(II) a2k+1=a2k+3k = a2k-1+(-1)k+3k, 所以a2k+1-a2k-1=3k+(-1)k,
同理a2k-1-a2k-3=3k-1+(-1)k-1, a3-a1=3+(-1).
所以(a2k+1-a2k-1)+(a2k-1-a2k-3)+…+(a3-a1)
=(3k+3k-1+…+3)+[(-1)k+(-1)k-1+…+(-1)],
由此得a2k+1-a1= (3k-1)+
(3k-1)+ [(-1)k-1],
[(-1)k-1],
于是a2k+1= a2k=
a2k-1+(-1)k=
a2k=
a2k-1+(-1)k= (-1)k-1-1+(-1)k=
(-1)k-1-1+(-1)k= (-1)k=1.
(-1)k=1.
{an}的通項公式為:
當n為奇數時,an=
當n為偶數時,
(四)用函數方法解題
8、(04年天津)已知數列{an},那么“對任意的n N+,點Pn(n ,an)都在直線y=x+1上”是“{an}為等差數列”的( B)
N+,點Pn(n ,an)都在直線y=x+1上”是“{an}為等差數列”的( B)
A必要條件 B 充分條件 C 充要條件 D 既不充分也不必要條件
9、(99年上海)已知等差數列{an}滿足3a4=7a7,且a1>0,Sn是{an}的前n項和,Sn取得最大值,則n=___9______.
10、(01年上海)已知數列{an}中an=2n-7,(n N+),
N+), +
+ +--+
+--+ =_153___
=_153___
(三)用整體化方法解題
5、(00年)已知等差數列{an}滿足a1+a2+a3+…+a101=0,則有(C )
A a1+a101>0 B a2+a100<0 C a3+a99=0 D a51=51
6、(02年)若一個等差數列的前3項和為34,最后3項的和為146,且所有項的和為390,則這個數列的項數為(A)
A 13 B 12 C 11 D 10
7、(03年上海)在等差數列{an}中a5=3,a6=-2,a4+a5+…+a10=-49
(二)用賦值法解題
2、(96年)等差數列{an}的前m項和為30,前2m項和為100,則它的前3m項和為(C )
A
130
B 170 C 210 D
260
3、(01年)設{an}是公比為q的等比數列, Sn是{an}的前n項和,若{Sn}是等差數列,則q=__1_
4、設數列{an}的前項的和Sn= (對于所有n
(對于所有n 1),且a4=54,則a1=__2___
1),且a4=54,則a1=__2___
(一)用基本量方法解題
1、(04年浙江)已知等差數列的公差為2,若a1,a3,a4成等比數列,則a2= (B )
A -4 B -6 C -8 D -10
例1.已知數列{a }是公差d≠0的等差數列,其前n項和為S
}是公差d≠0的等差數列,其前n項和為S .
.
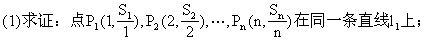

(2)過點Q (1,a
(1,a ),Q
),Q (2,a
(2,a )作直線12,設l
)作直線12,設l 與l
與l 的夾角為θ,
的夾角為θ,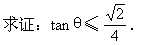

證明:(1)因為等差數列{a }的公差d≠0,所以
}的公差d≠0,所以
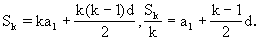

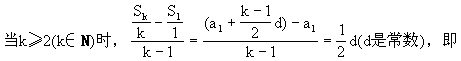

Kp p
p 是常數(k=2,3,…,n).
是常數(k=2,3,…,n).
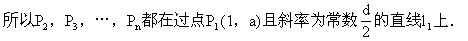

(2)直線l 的方程為y-a
的方程為y-a =d(x-1),直線l
=d(x-1),直線l 的斜率為d.
的斜率為d.
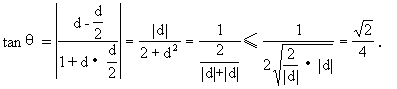

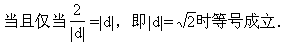

例2.已知數列 中,
中, 是其前
是其前 項和,并且
項和,并且 ,
,
⑴設數列 ,求證:數列
,求證:數列 是等比數列;
是等比數列;
⑵設數列 ,求證:數列
,求證:數列 是等差數列;
是等差數列;
⑶求數列 的通項公式及前
的通項公式及前 項和。
項和。
分析:由于{b }和{c
}和{c }中的項都和{a
}中的項都和{a }中的項有關,{a
}中的項有關,{a }中又有S
}中又有S =4a
=4a +2,可由S
+2,可由S -S
-S 作切入點探索解題的途徑.
作切入點探索解題的途徑.
解:(1)由S =4a
=4a ,S
,S =4a
=4a +2,兩式相減,得S
+2,兩式相減,得S -S
-S =4(a
=4(a -a
-a ),即a
),即a =4a
=4a -4a
-4a .(根據b
.(根據b 的構造,如何把該式表示成b
的構造,如何把該式表示成b 與b
與b 的關系是證明的關鍵,注意加強恒等變形能力的訓練)
的關系是證明的關鍵,注意加強恒等變形能力的訓練)
a -2a
-2a =2(a
=2(a -2a
-2a ),又b
),又b =a
=a -2a
-2a ,所以b
,所以b =2b
=2b ①
①
已知S =4a
=4a +2,a
+2,a =1,a
=1,a +a
+a =4a
=4a +2,解得a
+2,解得a =5,b
=5,b =a
=a -2a
-2a =3 ②
=3 ②
由①和②得,數列{b }是首項為3,公比為2的等比數列,故b
}是首項為3,公比為2的等比數列,故b =3·2
=3·2 .
.
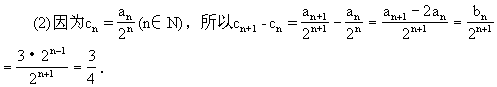

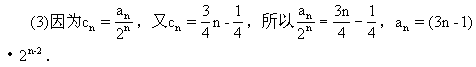
當n≥2時,S =4a
=4a +2=2
+2=2 (3n-4)+2;當n=1時,S
(3n-4)+2;當n=1時,S =a
=a =1也適合上式.
=1也適合上式.
綜上可知,所求的求和公式為S =2
=2 (3n-4)+2.
(3n-4)+2.
說明:1.本例主要復習用等差、等比數列的定義證明一個數列為等差,等比數列,求數列通項與前 項和。解決本題的關鍵在于由條件
項和。解決本題的關鍵在于由條件 得出遞推公式。
得出遞推公式。
2.解綜合題要總攬全局,尤其要注意上一問的結論可作為下面論證的已知條件,在后面求解的過程中適時應用.
例3.(04年浙江)設數列{an}的前項的和Sn= (an-1) (n
(an-1) (n +),(1)求a1;a2; (2)求證數列{an}為等比數列。
+),(1)求a1;a2; (2)求證數列{an}為等比數列。
解: (Ⅰ)由 ,得
,得 ∴
∴
 又
又 ,即
,即 ,得
,得 .
.
(Ⅱ)當n>1時,
得 所以
所以 是首項
是首項 ,公比為
,公比為 的等比數列.
的等比數列.
例4、(04年重慶)設a1=1,a2= ,an+2=
,an+2= an+1-
an+1- an (n=1,2,---),令bn=an+1-an (n=1,2---)求數列{bn}的通項公式,(2)求數列{nan}的前n項的和Sn。
an (n=1,2,---),令bn=an+1-an (n=1,2---)求數列{bn}的通項公式,(2)求數列{nan}的前n項的和Sn。
解:(I)因

故{bn}是公比為 的等比數列,且
的等比數列,且

(II)由


注意到 可得
可得
記數列 的前n項和為Tn,則
的前n項和為Tn,則



例5.在直角坐標平面上有一點列 ,對一切正整數
,對一切正整數 ,點
,點 位于函數
位于函數 的圖象上,且
的圖象上,且 的橫坐標構成以
的橫坐標構成以 為首項,
為首項, 為公差的等差數列
為公差的等差數列 。
。
⑴求點 的坐標;
的坐標;
⑵設拋物線列 中的每一條的對稱軸都垂直于
中的每一條的對稱軸都垂直于 軸,第
軸,第 條拋物線
條拋物線 的頂點為
的頂點為 ,且過點
,且過點 ,記與拋物線
,記與拋物線 相切于
相切于 的直線的斜率為
的直線的斜率為 ,求:
,求: 。
。
⑶設 ,等差數列
,等差數列 的任一項
的任一項 ,其中
,其中 是
是 中的最大數,
中的最大數, ,求
,求 的通項公式。
的通項公式。
解:(1)

(2) 的對稱軸垂直于
的對稱軸垂直于 軸,且頂點為
軸,且頂點為 .
. 設
設 的方程為:
的方程為:
把 代入上式,得
代入上式,得 ,
, 的方程為:
的方程為: 。
。
 ,
,


=
(3) ,
,


 T中最大數
T中最大數 .
.
設 公差為
公差為 ,則
,則 ,由此得
,由此得

說明:本例為數列與解析幾何的綜合題,難度較大(1)、(2)兩問運用幾何知識算出 ,解決(3)的關鍵在于算出
,解決(3)的關鍵在于算出 及求數列
及求數列 的公差。
的公差。
例6.數列 中,
中, 且滿足
且滿足

⑴求數列 的通項公式;
的通項公式;
⑵設 ,求
,求 ;
;
⑶設 =
=
 ,是否存在最大的整數
,是否存在最大的整數 ,使得對任意
,使得對任意 ,均有
,均有
 成立?若存在,求出
成立?若存在,求出 的值;若不存在,請說明理由。
的值;若不存在,請說明理由。
解:(1)由題意, ,
, 為等差數列,設公差為
為等差數列,設公差為 ,
,
由題意得 ,
, .
.
(2)若 ,
,

 時,
時,

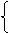 故
故


(3)




若 對任意
對任意 成立,即
成立,即 對任意
對任意 成立,
成立,
 的最小值是
的最小值是 ,
,
 的最大整數值是7。
的最大整數值是7。
即存在最大整數 使對任意
使對任意 ,均有
,均有
說明:本例復習數列通項,數列求和以及有關數列與不等式的綜合問題.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com