
9.(浙江卷7)若雙曲線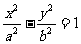 的兩個焦點到一條準線的距離之比為3:2,則雙曲線的離心率是
的兩個焦點到一條準線的距離之比為3:2,則雙曲線的離心率是
8.(天津卷(7)設橢圓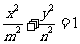 (
(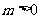 ,
,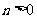 )的右焦點與拋物線
)的右焦點與拋物線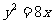 的焦點相同,離心率為
的焦點相同,離心率為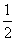 ,則此橢圓的方程為
,則此橢圓的方程為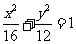
7.(陜西卷8)雙曲線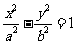 (
(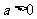 ,
,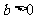 )的左、右焦點分別是
)的左、右焦點分別是 ,過
,過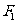 作傾斜角為
作傾斜角為 的直線交雙曲線右支于
的直線交雙曲線右支于 點,若
點,若 垂直于
垂直于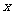 軸,則雙曲線的離心率為
軸,則雙曲線的離心率為
6.(山東卷(10)設橢圓C1的離心率為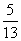 ,焦點在x軸上且長軸長為26.若曲線C2上的點到橢圓C1的兩個焦點的距離的差的絕對值等于8,則曲線C2的標準方程為
,焦點在x軸上且長軸長為26.若曲線C2上的點到橢圓C1的兩個焦點的距離的差的絕對值等于8,則曲線C2的標準方程為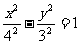
5.(全國二9)設 ,則雙曲線
,則雙曲線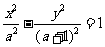 的離心率
的離心率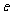 的取值范圍是
的取值范圍是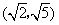
4.(江西卷7)已知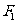 、
、 是橢圓的兩個焦點,滿足
是橢圓的兩個焦點,滿足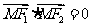 的點
的點 總在橢圓內部,則橢圓離心率的取值范圍是
總在橢圓內部,則橢圓離心率的取值范圍是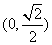
3.(湖南卷8)若雙曲線 (a>0,b>0)上橫坐標為
(a>0,b>0)上橫坐標為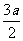 的點到右焦點的距離大于它到左準線的距離,則雙曲線離心率的取值范圍是(2,+
的點到右焦點的距離大于它到左準線的距離,則雙曲線離心率的取值范圍是(2,+ )
)
2.(海南卷11)已知點P在拋物線y2 =
4x上,那么點P到點Q(2,-1)的距離與點P到拋物線焦點距離之和取得最小值時,點P的坐標為(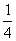 ,-1)
,-1)
(1)會利用方程組解的狀況確定直線與圓錐曲線的位置關系;
(2)會求直線被圓錐曲線所截的弦長,弦的中點坐標:
如:設拋物線經過兩點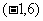 和
和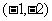 ,對稱軸與
,對稱軸與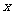 軸平行,開口向右,直線
軸平行,開口向右,直線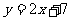 被拋物線截得的線段長是
被拋物線截得的線段長是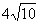 ,求拋物線方程。
,求拋物線方程。
(3)當直線與圓錐曲線相交時,求在某些給定條件下地直線線方程;解此類問題,一般是根據條件求解,但要注意 條件的應用。
條件的應用。
如:已知拋物線方程為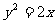 在
在 軸上截距為2的直線
軸上截距為2的直線 與拋物線交于
與拋物線交于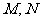 兩點,且以
兩點,且以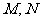 為徑的圓過原點,求直線
為徑的圓過原點,求直線 的方程。
的方程。
課本題P26練習1(3)(4)3;習題2(3)(4)3,4;P30練習2(3)(4)4;
P31習題5,7,10;P34練習5,6,7;P38練習2,3;P39 習題5,6,7;P42
練習4,5;P44 習題5,6,7;P47 習題8,9,11,12,13,16,17,18,19,21;
高考題
1.(福建卷11)又曲線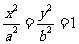 (a>0,b>0)的兩個焦點為F1、F2,若P為其上一點,且|PF1|=2|PF2|,則雙曲線離心率的取值范圍為
(a>0,b>0)的兩個焦點為F1、F2,若P為其上一點,且|PF1|=2|PF2|,則雙曲線離心率的取值范圍為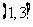
(1)直接法: 已知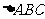 底邊
底邊 的長為8,兩底角之和為
的長為8,兩底角之和為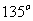 ,求頂點且的軌跡方程。
,求頂點且的軌跡方程。
(2)定義法:已知圓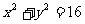 ,定點
,定點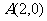 ,若
,若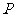 是圓上的動點,
是圓上的動點,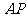 的垂直平分線交
的垂直平分線交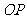 于
于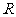 ,求
,求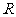 的軌跡方程。
的軌跡方程。
(3)幾何法: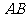 是
是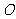 的直徑,且
的直徑,且 ,
, 為圓上一動點,作
為圓上一動點,作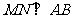 ,垂足為
,垂足為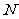 ,在
,在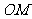 上取點
上取點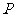 ,使
,使 ,求點
,求點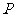 的軌跡。
的軌跡。
(4)相關點法(代人法) 在雙曲線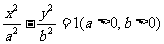 的兩條漸近線上分別取點
的兩條漸近線上分別取點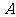 和
和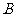 ,使
,使 (其中
(其中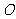 為坐標原點,
為坐標原點,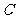 為雙曲線的半焦距),求
為雙曲線的半焦距),求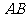 中點的軌跡。
中點的軌跡。
(5)整體法(設而不求法):以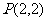 為圓心的圓與橢圓
為圓心的圓與橢圓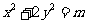 交于
交于 兩點,求
兩點,求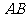 中點
中點 的軌跡方程。
的軌跡方程。
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com