
2.當總體中個體取不同值很少時,我們黨用樣本的頻率分布標記頻率分布梯形圖取估計總體體分布,總體分布排除了抽樣造成的錯誤,精確反映了總體取值的概率分布規律。對于所取不同數值較多或可以在實數區間范圍內取值的總體,需用頻率分布直方圖來表示相應的頻率分布。當樣本容量無限增大,分組的組距無限縮小時,頻率分布直方圖無限接近一條光滑曲線--總體密度曲線.由于總體分布通常不易知道,往往是用樣本的頻率分布估計總體分布。樣本容量越大,估計就越精確
1.統計是為了從數據中提取信息,學習時根據實際問題的需求選擇不同的方法合理地選取樣本,并從樣本數據中提取需要的數字特征。不應把統計處理成數字運算和畫圖表。對統計中的概念(如"總體"、"樣本"等)應結合具體問題進行描述性說明,不應追求嚴格的形式化定義
9.4 8.4 9.4 9.9 9.6 9.4 9.7
去掉一個最高分和一個最低分后,所剩數據的平均值和方差分別為
(A)9.4, 0.484 (B)9.4, 0.016 (C)9.5, 0.04 (D)9.5, 0.016
答案:D;
解析:7個數據中去掉一個最高分和一個最低分后,余下的5個數為:9.4, 9.4, 9.6, 9.4, 9.5。
則平均數為: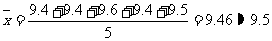 ,即
,即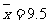 。
。
方差為: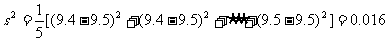
即
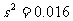 ,故選D。
,故選D。
點評:一定要根據實際的題意解決問題,并還原實際情景
題型3:頻率分布直方圖與條形圖
例5.為檢測,某種產品的質量,抽取了一個容量為30的樣本,檢測結果為一級品5件,而極品8件,三級品13件,次品14件.
(1)列出樣本頻率分布表;
(2)畫出表示樣本頻率分布的條形圖;
(3)根據上述結果,估計辭呈商品為二極品或三極品的概率約是多少
解析:(1)樣本的頻率分布表為
|
產品 |
頻數 |
頻率 |
|
一級品 |
5 |
0.17 |
|
二級品 |
8 |
0.27 |
|
三級品 |
13 |
0.43 |
|
次品 |
4 |
0.13 |
(2)樣本頻率分布的條形圖為:
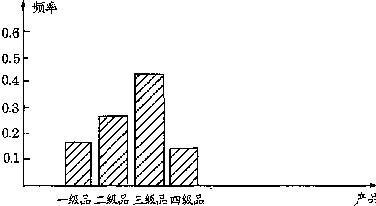
(3)此種產品為二極品或三極品的概率約為0.27+0.43=0.7。
點評:條形圖中縱坐標一般是頻數或頻率
例6.為了了解某地區高三學生的身體發育情況,抽查了該地區100名年齡為17.5歲-18歲的男生體重(kg) ,得到頻率分布直方圖如下:
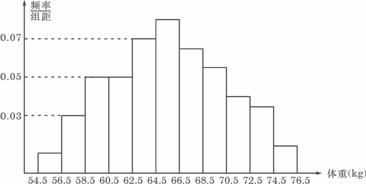
根據上圖可得這100名學生中體重在(56.5,64.5)的學生人數是
(A)20 (B)30
(C)40 (D)50
答案:C;
解析:根據運算的算式:體重在(56.5,64.5)學生的累積頻率為2×0.03+2×0.05+2×0.05+2×0.07=0.4,則體重在(56.5,64.5)學生的人數為0.4×100=40。
點評:熟悉頻率、頻數、組距間的關系式。
例7.某中學對高三年級進行身高統計,測量隨機抽取的40名學生的身高,其結果如下(單位:cm)
|
分組 |
[140,145) |
[145,150) |
[150,155) |
[155,160) |
[160,165) |
[165,170) |
[170,175) |
[175,180) |
合計 |
人 數 數 |
1 |
2 |
5 |
9 |
13 |
6 |
3 |
1 |
40 |
(1)列出頻率分布表;
(2)畫出頻率分布直方圖;
(3)估計數據落在[150,170]范圍內的概率
解析:(1)根據題意可列出頻率分布表:
|
分 值 |
頻 數 |
頻 率 |
|
[140,145] |
1 |
0.025 |
|
[145,150] |
2 |
0.050 |
|
[150,155] |
5 |
0.125 |
|
[155,160] |
9 |
0.225 |
|
[160,165] |
13 |
0.325 |
|
[165,170] |
6 |
0.15 |
|
[170,175] |
3 |
0.075 |
|
[175,180] |
1 |
0.025 |
|
合 計 |
40 |
1.00 |
(2)頻率分布直方圖如下:
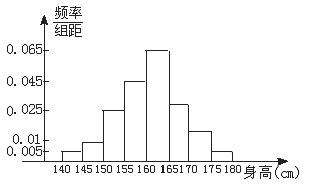
(3)數據落在[150,170]范圍內的概率約為0.825。
題型4:莖葉圖
例8.觀看下面兩名選手全壘打數據的莖葉圖,對他們的表現進行比較。
1961年揚基隊外壘手馬利斯打破了魯斯的一個賽季打出60個全壘打的記錄。下面是揚基隊的歷年比賽中的魯斯和馬利斯每年擊出的全壘打的比較圖:
魯斯 馬利斯
0 8
1 3 4 6
5 2 2 3 6 8
5 4 3 3 9
9 7 6 6 1 1 4
9 4 4 5
0 6 1
解析:魯斯的成績相對集中,穩定在46左右;馬利斯成績相對發散,成績穩定在26左右。
題型5:線性回歸方程
例9.由施肥量x與水稻產量y試驗數據的關系,畫出散點圖,并指明相關性。

解析:散點圖為:
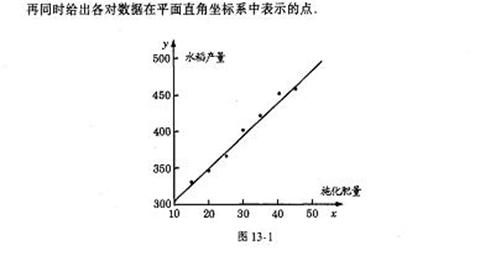
通過圖象可知是正相 關。
關。
例10.在某種產品表面進行腐蝕線實驗,得到腐蝕深度y與腐蝕時間t之間對應的一組數據:
|
時間t(s) |
5 |
10 |
15 |
20 |
30 |
40 |
50 |
60 |
70 |
90 |
120 |
深度y(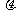 m) m) |
6 |
10 |
10 |
13 |
16 |
17 |
19 |
23 |
25 |
29 |
46 |
(1)畫出散點圖;
(2)試求腐蝕深度y對時間t的回歸直線方程。
略解:(1)散點圖略,呈直線形
(2)經計算可得
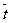 =46.36,
=46.36,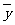 =19.45,
=19.45,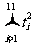 =36750,
=36750,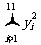 =5442,
=5442,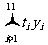 =13910。
=13910。
B=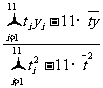 =
=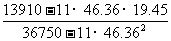
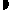 0.3.
0.3.
A=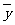 -b
-b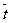 =19.45-03
=19.45-03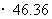
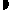 5.542。
5.542。
故所求的回歸直線方程為 =0.3t+5.542。
=0.3t+5.542。
題型6:創新題
例11.把容量為100的某個樣本數據分為10組,并填寫頻率分布表,若前七組的累積頻率為0.79,而剩下三組的頻數成公比大于2的整數等比數列,則剩下三組中頻數最高的一組的頻數為___________.
答案:16
點評:已知前七組的累積頻率為0.79,而要研究后三組的問題,因此應先求出后三組的頻率之和為1-0.79=0.21,進而求出后三組的共有頻數,或者先求前七組共有頻數后,再計算后三組的共有頻數。由已知知前七組的累積頻數為0.79×100=79,故后三組共有的頻數為21,依題意 =21,a1(1+q+q2)=21.∴a1=1,q=4。∴后三組頻數最高的一組的頻數為16。此題剖析只按第二種思路給出了解答,你能按第一種思路來解嗎?
=21,a1(1+q+q2)=21.∴a1=1,q=4。∴后三組頻數最高的一組的頻數為16。此題剖析只按第二種思路給出了解答,你能按第一種思路來解嗎?
例12.某班學生在一次數學考試中成績分布如下表:
|
分數段 |
[0,80) |
[80,90) |
[90,100) |
||
|
人數 |
2 |
|
6 |
||
|
分數段 |
[100,110) |
[110,120 |
[120,130) |
||
|
人數 |
8 |
12 |
6 |
||
|
分數段 |
[130,140) |
[140,150) |
|
||
|
人數 |
4 |
2 |
|
那么分數在[100,110)中的頻率和分數不滿110分的累積頻率分別是______________、_______(精確到0.01).
解析:由頻率計算方法知:總人數=45.
分數在[100,110)中的頻率為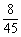 =0.178≈0.18.
=0.178≈0.18.
分數不滿110分的累積頻率為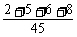 =
=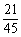 ≈0.47.
≈0.47.
答案:0.18 0.47
(2009湖北卷文)下圖是樣本容量為200的頻率分布
直方圖.
根據樣本的頻率分布直方圖估計,樣本數據落在[6,10]內的頻數為 ,數據落在(2,10)內的概率約為 。
答案 64
解析 觀察直方圖易得頻數為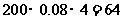 ,
,
頻率為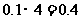
1.7 1.2 2.1 3.2 1.0
(1)通過對樣本的計算,估計該縣1999年消耗了多少盒一次性筷子(每年按350個營業日計算);
(2)2001年又對該縣一次性木質筷子的用量以同樣的方式作了抽樣調查,調查的結果是10個樣本飯店,每個飯店平均每天使用一次性筷子2.42盒.求該縣2000年、2001年這兩年一次性木質筷子用量平均每年增長的百分率(2001年該縣飯店數、全年營業天數均與1999年相同);
(3)在(2)的條件下,若生產一套學生桌椅需木材0.07m3,求該縣2001年使用一次性筷子的木材可以生產多少套學生桌椅。計算中需用的有關數據為:每盒筷子100雙,每雙筷子的質量為5g,所用木材的密度為0.5×103kg/m3;
(4)假如讓你統計你所在省一年使用一次性筷子所消耗的木材量,如何利用統計知識去做,簡要地用文字表述出來。
解析:(1)
所以,該縣1999年消耗一次性筷子為2×600×350=420000(盒)。
(2)設平均每年增長的百分率為X,則2(1+X)2=2.42,
解得X1=0.1=10%,X2=-2.1(不合題意,舍去)。
所以,平均每年增長的百分率為10%;
(3)可以生產學生桌椅套數為 (套)。
(套)。
(2009四川卷文)設矩形的長為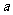 ,寬為
,寬為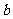 ,其比滿足
,其比滿足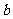 ∶
∶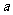 =
=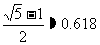 ,這種矩形給人以美感,稱為黃金矩形。黃金矩形常應用于工藝品設計中。下面是某工藝品廠隨機抽取兩個批次的初加工矩形寬度與長度的比值樣本:
,這種矩形給人以美感,稱為黃金矩形。黃金矩形常應用于工藝品設計中。下面是某工藝品廠隨機抽取兩個批次的初加工矩形寬度與長度的比值樣本:
甲批次:0.598 0.625 0.628 0.595 0.63 9
9
乙批次:0.618 0.6 13
0.592 0.622
13
0.592 0.622 0.620
0.620
根據上述兩個樣本來估計兩個批次的總體平均數,與標準值0.618比較,正確結論是
A.甲批次的總體平均數與標準值更接近
B.乙批次的總體平均數與標準值更接近
C.兩個批次總體平均數與標準值接近程度相同
D .兩個批次總體平均數與標準值接近程度不能確定
.兩個批次總體平均數與標準值接近程度不能確定
答案 A
解析 甲批次的平均數為0.617,乙批次的平均數為0.613
(4)先抽取若干個縣(或市、州)作樣本,再分別從這些縣(或市、州)中抽取若干家飯店作樣本,統計一次性筷子的用量.
點評:本題是一道統計綜合題,涉及的知識點很多,需要 靈活運用各種知識分析解決問題.對于第(1)小題,可先求得樣本平均數,再利用樣本估計總體的思想來求得問題的解.對于第(2)小題,實際是一個增長率問題的應用題,可通過設未知數列方程的方法來解.對于第(3)小題,用到了物理公式m=ρv, 體現了各學科知識之間的聯系,讓學生觸類旁通,在解決實際問題時能綜合運用多種知識靈活地解決問題.第(4)小題只要能夠運用隨機抽樣方法,能體會到用樣本估計總體的統計思想就可解決,在文字表述上要注意簡潔、明了、正確。
靈活運用各種知識分析解決問題.對于第(1)小題,可先求得樣本平均數,再利用樣本估計總體的思想來求得問題的解.對于第(2)小題,實際是一個增長率問題的應用題,可通過設未知數列方程的方法來解.對于第(3)小題,用到了物理公式m=ρv, 體現了各學科知識之間的聯系,讓學生觸類旁通,在解決實際問題時能綜合運用多種知識靈活地解決問題.第(4)小題只要能夠運用隨機抽樣方法,能體會到用樣本估計總體的統計思想就可解決,在文字表述上要注意簡潔、明了、正確。
題型2:數字特征的應用
例3.甲、乙兩種冬小麥試驗品種連續5年的平均單位面積產量如下(單位:t / hm2)
|
品種 |
第1年 |
第2年 |
第3年 |
第4年 |
第5年 |
|
甲 |
9.8 |
9.9 |
10. 1 1 |
10 |
10.2 |
|
乙 |
9.4 |
10.3 |
10.8 |
9.7 |
9.8 |
其中產量比較穩定的小麥品種是 甲 。
解析:¯甲 = 1 5( 9.8 + 9.9 + 10.1 + 10 + 10.2) = 10.0,¯乙 = 1 5( 9.4 + 10.3 + 10.8 + 9.7 + 9.8) = 10.0;
s 2甲 = 1 5( 9.82 + … + 10.22) – 102 = 0.02,s 2甲 = 1 5( 9.42 + … + 9.82) – 102 = 0.244 > 0.02 。
點評:方差與平均數在反映樣本的特征上一定要區分開
例4.在一次歌手大獎賽上,七位評委為歌手打出的分數如下:
題型1:數字特征
例1.為了檢查一批手榴彈的殺傷半徑,抽取了其中20顆做試驗,得到這20顆手榴彈的殺傷半徑,并列表如下:

(1)在這個問題中,總體、個體、樣本和樣本容量各是什么?
(2)求出這20顆手榴彈的殺傷半徑的眾數、中位數和平均數,并估計這批手榴彈的平均殺傷半徑.
解析: (1)總體是要檢查的這批手榴彈的殺傷半徑的全體;個體是每一顆手榴彈的殺傷半徑;樣本是所抽取的20顆手榴彈的殺傷半徑;樣本容量是20。
(2)在20個數據中,10出現了6次,次數最多,所以眾數是10(米)
20個數據從小到大排列,第10個和第11個數據是最中間的兩個數,分別為9(米)和10(米),所以中位數是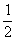 (9+10)=9.5(米)。
(9+10)=9.5(米)。
樣本平均數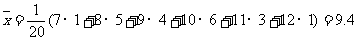 (米)
(米)
所以,估計這批手榴彈的平均殺傷半徑約為9.4米。
點評:(1)根據總體、個體、樣本、樣本容量的概念答題.要注意:總體、個體和樣本所說的考察對象是一種數量指標,不能說成考察的對象是手榴彈,而應說是手榴彈的殺傷半徑。
(2009山東卷理)某工廠對一批產品進行了抽樣 檢測.右圖是根據抽樣檢測后的
檢測.右圖是根據抽樣檢測后的
產品凈重(單位:克)數據繪制的頻率分布直方圖,其中產品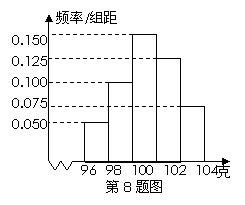
凈重的范圍是[96,106],樣本數據分組為[96,98),[98,100),
[100,102),[102,104),[104,106],已知樣本中產品凈重小于
100克的個數是36,則樣本中凈重大于或等于98克并且
小于104克的產品的個數是 ( ).
A.90 B.75 C. 60 D.45
答案 A
解析 產品凈重小于100克的概率為(0.050+0.100)×2=0.300,
已知樣本中產品凈重小于100克的個數是36,設樣本容量為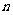 ,
,
則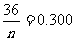 ,所以
,所以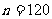 ,凈重大于或等于98克并且小于
,凈重大于或等于98克并且小于
104克的產品的概率為(0.100+0.150+0.125)×2=0.75,所以樣本
中凈重大于或等于98克并且小于104克的產品的個數是
120×0.75=90.故選A.
[命題立意]:本題考查了統計與概率的知識,讀懂頻率分布直方圖,會計算概率以及樣本中有關的數據.
(2)讀懂表格的意義,利用概念求眾數、中位數,用 樣本平均數估計這批手榴彈的平均殺傷半徑.另外在這里要會簡便計算有多個重復數據的樣本的平均數。
樣本平均數估計這批手榴彈的平均殺傷半徑.另外在這里要會簡便計算有多個重復數據的樣本的平均數。
例2.為估計一次性木質筷子的用量,1999年從某縣共600家高、中、低檔飯店抽取10家作樣本,這些飯店每天消耗的一次性筷子盒數分別為:
0.6 3.7 2.2 1.5 2.8
3.線性回歸
回歸分析:對于兩個變量,當自變量取值一定時,因變量的取值帶有一定隨機性的兩個變量之間的關系叫相關關系或回歸關系。
回歸直線方程:設x與y是具有相關關系的兩個變量,且相應于n個觀測值的n個點大致分布在某一條直線的附近,就可以認為y對x的回歸函數的類型為直線型: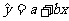 。其中
。其中 ,
,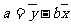 。我們稱這個方程為y對x的回歸直線方程。
。我們稱這個方程為y對x的回歸直線方程。
2.頻率分布直方圖、折線圖與莖葉圖
樣本中所有數據(或數據組)的頻率和樣本容量的比,就是該數據的頻率。所有數據(或數據組)的頻率的分布變化規律叫做頻率分布,可以用頻率分布直方圖、折線圖、莖葉圖來表示。
頻率分布直方圖:
具體做法如下:
(1)求極差(即一組數據中最大值與最小值的差);
(2)決定組距與組數;
(3)將數據分組;
(4)列頻率分布表;
(5)畫頻率分布直方圖
注:頻率分布直方圖中小正方形的面積=組距× =頻率。
=頻率。
折線圖:連接頻率分布直方圖中小長方形上端中點,就得到頻率分布折線圖
總體密度曲線:當樣本容量足夠大,分組越多,折線越接近于一條光滑的曲線,此滑曲線為總體密度曲線。
1.用樣本的數字特征估計總體的數字特征
(1)眾數、中位數
在一組數據中出現次數最多的數據叫做這組數據的眾數;
將一組數據按照從大到小(或從小到大)排列,處在中間位置上的一個數據(或中間兩位數據的平均數)叫做這組數據的中位數;
(2)平均數與方差
如果這n個數據是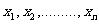 ,那么
,那么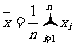 叫做這n個數據平均數;
叫做這n個數據平均數;
如果這n個數據是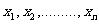 ,那么
,那么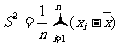 叫做這n個數據方差;同時
叫做這n個數據方差;同時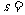
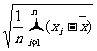 叫做這n個數據的標準差。
叫做這n個數據的標準差。
2.熱點問題是頻率分布直方圖和用樣本的數字特征估計總體的數字特征。
“統計”是在初中“統計初步”基礎上的深化和擴展,本講主要會用樣本的頻率分布估計總體的分布,并會用樣本的特征來估計總體的分布
預測2011年高考對本講的考察是:
1.以基本題目(中、低檔題)為主,多以選擇題、填空題的形式出現,以實際問題為背景,綜合考察學生學習基礎知識、應用基礎知識、解決實際問題的能力;
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com