日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

3．已知正四棱柱ABCD-A₁B₁C₁D₁．AB=1，AA₁=2，點(diǎn)E為CC₁中點(diǎn)，點(diǎn)P為BD₁中點(diǎn)． 證明EF為BD₁與CC₁的公垂線(xiàn)；

證：建立如圖的坐標(biāo)系，得B(0，1，0)，D₁(1，0，2)，F(，，1)，C₁(0，0，2)，E(0，0，1)．

即EF⊥CC₁，EF⊥BD₁ ．

故EF是為BD₁ 與CC₁的公垂線(xiàn)．

2．設(shè)=(cosα，1，sinα)，=(sinα，1，cosα)，求證：(+)⊥(－)。

1．下列五個(gè)正方體圖形中，l是正方體的一條對(duì)角線(xiàn)，點(diǎn)M、N、P分別是其所在棱的中點(diǎn)，能得出l⊥平面MNP的圖形的序號(hào)是_____________．①④⑤．

7．已知向量=(3，0，1)，=(-1，1，2)，⊥，∥，若=－，求向量的坐標(biāo)。(-，1，)

考查空間向量的概念及運(yùn)算．要求空間向量的加法、減法和數(shù)乘、空間向量的坐標(biāo)運(yùn)算、空間向量的數(shù)量積的概念、性質(zhì)．

6．若e₁，e₂，e₃是三個(gè)不共面向量，試問(wèn)向量a=3e₁+2e₂+e₃，b=－e₁+ e ₂+3 e ₃，c=2e ₁－e ₂－4 e ₃是否共面，并說(shuō)明理由。

解：由共面向量定理可知，關(guān)鍵是能否找到三個(gè)不全為零的實(shí)數(shù)x，y，z，

使得xa+yb+zc=0，即x(3 e₁+2e₂+e₃)+y(－e₁+ e ₂+3 e ₃)+z(2 e ₁－e ₂－4 e ₃)=0，

即(3x－y+2z)e₁+(2x+y－z)e₂+(x+3y－4z)e₃=0。由于e₁，e₂，e₃不共面，

故得3x－y+2z=0，①　　 2x+y－z=0，②　　　 x+3y－4z=0。③

①+②求得z=－5x，代入③得y=－7x，取x=1，則y=－7，z=－5，于是a－7b－5c=0，

即a=7b+5c，所以a，b，c三向量共面。

5．已知、是空間兩個(gè)單位向量，它們的夾角為60°，設(shè)向量=2+，=－3+2，則向量與的夾角是_______．120°

4．命題：

①若a與b共線(xiàn)，b與c共線(xiàn)，則a與c共線(xiàn)；

②向量a、b、c共面，則它們所在的直線(xiàn)也共面；

③若a與b共線(xiàn)，則存在唯一的實(shí)數(shù)λ，使b=λa；

④若A、B、C三點(diǎn)不共線(xiàn)，O是平面ABC外一點(diǎn)，= + + ，

則點(diǎn)M一定在平面ABC上，且在△ABC內(nèi)部．

上述命題中的真命題是_____________．④

解：①中b為零向量時(shí)，a與c可以不共線(xiàn)，故①是假命題；②中a所在的直線(xiàn)其實(shí)不確定，故②是假命題；③中當(dāng)a=0，而b≠0時(shí)，則找不到實(shí)數(shù)λ，使b=λa，故③是假命題；④中M是△ABC的重心，故M在平面ABC上且在△ABC內(nèi)，故④是真命題．

3．下列命題中不正確的命題個(gè)數(shù)是　　　　　　　　　　　　　　　　　　 (　　　 )

①若A、B、C、D是空間任意四點(diǎn)，則有+++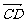=0;　

②|a|－|b|=|a+b|是a、b共線(xiàn)的充要條件;　

③若a、b共線(xiàn)，則a與b所在直線(xiàn)平行;　

④對(duì)空間任意點(diǎn)O與不共線(xiàn)的三點(diǎn)A、B、C，若=x+y+z(其中x、y、z∈R)，

則P、A、B、C四點(diǎn)共面　　　　　　　　　　　　　　　　　　　　　 (　 C　 )

A．1　　　 　　　　　　　 B．2　　　 　　　　　　　　 C．3　　　 　　　　　　　 D．4

2．設(shè)O，P，A，B為空間任意四個(gè)點(diǎn)，如果滿(mǎn)足=m+n，且m+n=1，則 ( A　 )

A．P在直線(xiàn)AB上　 　　　　　　　　　　　　　　　　　　 B．P不在直線(xiàn)AB上

C．P有可能在直線(xiàn)AB上　 　　　　　　　　　　　　　　 D．以上都不對(duì)

1．在以下命題中:

①若a、b共線(xiàn)，則a與b所在直線(xiàn)平行

②若a，b所在直線(xiàn)是異面直線(xiàn)，則a與b一定不共面

③若a，b，c三向量?jī)蓛晒裁妫瑒ta，b，c三向量一定也共面

④若a，b，c三向量共面，則由a，b所在直線(xiàn)所確定的平面與由b，c所在直線(xiàn)所確定的平面一定平行。正確命題的個(gè)數(shù)為　　　　　　　　　　　　　　　　　　 ( A　 )

A．0　　　　 　　　　　　　 B．1　　　　 　　　　　　 C．2　　　　 　　　　　　　 D．3