
 如圖,平面直角坐標系中,矩形OABC的頂點B在第一象限,點C在x軸上,點A在y軸上,D、E分別是AB,OA中點.過點D的雙曲線y=$\frac{k}{x}$(x>0,k>0)與BC交于點G.連接DC,F在DC上,且DF:FC=3:1,連接DE,EF.若△DEF的面積為6,則k的值為( )
如圖,平面直角坐標系中,矩形OABC的頂點B在第一象限,點C在x軸上,點A在y軸上,D、E分別是AB,OA中點.過點D的雙曲線y=$\frac{k}{x}$(x>0,k>0)與BC交于點G.連接DC,F在DC上,且DF:FC=3:1,連接DE,EF.若△DEF的面積為6,則k的值為( )| A. | $\frac{16}{3}$ | B. | $\frac{32}{3}$ | C. | 6 | D. | 10 |
分析 設矩形OABC中OA=2a、AB=2b,由D、E分別是AB,OA中點知點D(b,2a)、E(0,a),過點F作FP⊥BC于點P,延長PF交OA于點Q,可得四邊形OCPQ是矩形,即OQ=PC、PQ=OC=2b,證△CFP∽△CDB得$\frac{CP}{CB}$=$\frac{FP}{DB}$=$\frac{CF}{CD}$,可得CP=$\frac{a}{2}$,FP=$\frac{b}{4}$、EQ=EO-OQ=$\frac{a}{2}$、FQ=PQ-PF=$\frac{7b}{4}$,根據S梯形ADFQ-S△ADE-S△EFQ=6求得ab即可得答案.
解答 解:設矩形OABC中OA=2a,AB=2b,
∵D、E分別是AB,OA中點,
∴點D(b,2a)、E(0,a),
如圖,過點F作FP⊥BC于點P,延長PF交OA于點Q,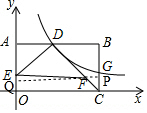
∵四邊形OABC是矩形,
∴∠QOC=∠OCP=∠CPQ=90°,
∴四邊形OCPQ是矩形,
∴OQ=PC,PQ=OC=2b,
∵FP⊥BC、AB⊥BC,
∴FP∥DB,
∴△CFP∽△CDB,
∴$\frac{CP}{CB}$=$\frac{FP}{DB}$=$\frac{CF}{CD}$,即$\frac{CP}{2a}=\frac{FP}{b}=\frac{1}{4}$,
可得CP=$\frac{a}{2}$,FP=$\frac{b}{4}$,
則EQ=EO-OQ=a-$\frac{a}{2}$=$\frac{a}{2}$,FQ=PQ-PF=2b-$\frac{b}{4}$=$\frac{7b}{4}$,
∵△DEF的面積為6,
∴S梯形ADFQ-S△ADE-S△EFQ=6,
即$\frac{1}{2}$•(b+$\frac{7}{4}$b)•$\frac{3}{2}$a-$\frac{1}{2}$ab-$\frac{1}{2}$×$\frac{7}{4}$b•$\frac{a}{2}$=6,
可得ab=$\frac{16}{3}$,
則k=2ab=$\frac{32}{3}$,
故選:B
點評 本題主要考查反比例函數系數的幾何意義及相似三角形的判定與性質、矩形的判定與性質及三角形的面積,利用相似三角形的判定與性質表示出點F的坐標是解題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
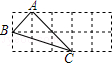 如圖,在5×2方格紙中,有一個以格點為頂點的△ABC,請你找出方格紙中所有與△ABC成軸對稱且也以格點為頂點的三角形,這樣的三角形共有4個.
如圖,在5×2方格紙中,有一個以格點為頂點的△ABC,請你找出方格紙中所有與△ABC成軸對稱且也以格點為頂點的三角形,這樣的三角形共有4個.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
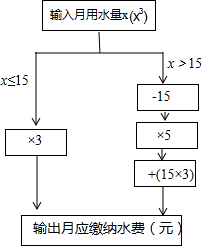 小明根據市自來水公司的居民用水收費標準,制定了如圖所示的水費計算數值轉換機示意圖,根據數值轉換機程序,小明輸入他家這個月的用水量,結果顯示應繳水費70元,那么小明家這個月的用水量為20m3.
小明根據市自來水公司的居民用水收費標準,制定了如圖所示的水費計算數值轉換機示意圖,根據數值轉換機程序,小明輸入他家這個月的用水量,結果顯示應繳水費70元,那么小明家這個月的用水量為20m3.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
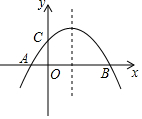 如圖,已知拋物線y=-$\frac{1}{m}$(x+2)(x-m)(m>0)與x軸相交于點A、B,與y軸相交于點C,且點A在點B的左側.
如圖,已知拋物線y=-$\frac{1}{m}$(x+2)(x-m)(m>0)與x軸相交于點A、B,與y軸相交于點C,且點A在點B的左側.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
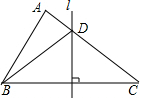 如圖,△ABC中,AB+AC=6cm,BC的垂直平分線l與AC相交于點D,則△ABD的周長為( )
如圖,△ABC中,AB+AC=6cm,BC的垂直平分線l與AC相交于點D,則△ABD的周長為( )| A. | 12cm | B. | 10cm | C. | 8cm | D. | 6cm |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com