
課 題: 10.1加法原理和乘法原理 (二)
教學目的:
1.進一步理解兩個基本原理.
2.會利用兩個原理分析和解決一些簡單的應用問題 
教學重點:兩個基本原理的進一步理解和體會
教學難點:正確判斷是分類還是分步,分類計數原理的分類標準及其多樣性
授課類型:新授課 
課時安排:1課時 
教 具:多媒體、實物投影儀 
教學過程:
一、復習引入:
1 分類計數原理:做一件事情,完成它可以有n類辦法,在第一類辦法中有
分類計數原理:做一件事情,完成它可以有n類辦法,在第一類辦法中有 種不同的方法,在第二類辦法中有
種不同的方法,在第二類辦法中有 種不同的方法,……,在第n類辦法中有
種不同的方法,……,在第n類辦法中有 種不同的方法
種不同的方法 那么完成這件事共有
那么完成這件事共有  種不同的方法
種不同的方法
2.分步計數原理:做一件事情,完成它需要分成n個步驟,做第一步有 種不同的方法,做第二步有
種不同的方法,做第二步有 種不同的方法,……,做第n步有
種不同的方法,……,做第n步有 種不同的方法,那么完成這件事有
種不同的方法,那么完成這件事有 種不同的方法
種不同的方法
3.原理淺釋
分類計數原理(加法原理)中,“完成一件事,有n類辦法”,是說每種辦法“互斥”,即每種方法都可以獨立地完成這件事,同時他們之間沒有重復也沒有遺漏.進行分類時,要求各類辦法彼此之間是相互排斥的,不論那一類辦法中的哪一種方法,都能獨立完成這件事.只有滿足這個條件,才能直接用加法原理,否則不可以.
分步計數原理(乘法原理)中,“完成一件事,需要分成n個步驟”,是說每個步驟都不足以完成這件事,這些步驟,彼此間也不能有重復和遺漏.
如果完成一件事需要分成幾個步驟,各步驟都不可缺少,需要依次完成所有步驟才能完成這件事,而各步要求相互獨立,即相對于前一步的每一種方法,下一步都有m種不同的方法,那么完成這件事的方法數就可以直接用乘法原理.
可以看出“分”是它們共同的特征,但是,分法卻大不相同.
兩個原理的公式是:  ,
, 
這種變形還提醒人們,分類和分步,常是在一定的限制之下人為的,因此,在這里我們大有用武之地:可以根據解題需要靈活而巧妙地分類或分步.
強調知識的綜合是近年的一種可取的現象.兩個原理,可以與物理中電路的串聯、并聯類比.
兩個基本原理的作用:計算做一件事完成它的所有不同的方法種數
兩個基本原理的區別:一個與分類有關,一個與分步有關;加法原理是“分類完成”,乘法原理是“分步完成”

二、講解范例:
解:取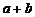 與取
與取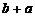 是同一種取法.分類標準為兩加數的奇偶性,第一類,偶偶相加,由分步計數原理得(10×9)/2=45種取法,第二類,奇奇相加,也有(10×9)/2=45種取法.根據分類計數原理共有45+45=90種不同取法.
是同一種取法.分類標準為兩加數的奇偶性,第一類,偶偶相加,由分步計數原理得(10×9)/2=45種取法,第二類,奇奇相加,也有(10×9)/2=45種取法.根據分類計數原理共有45+45=90種不同取法.
例2 在1~20共20個整數中取兩個數相加,使其和大于20的不同取法共有多少種?
解:分類標準一,固定小加數.小加數為1時,大加數只有20這1種取法;小加數為2時,大加數有19或20兩種取法;小加數為3時,大加數為18,19或20共3種取法…小加數為10時,大加數為11,12,…,20共10種取法;小加數為11時,大加數有9種取法…小加數取19時,大加數有1種取法.由分類計數原理,得不同取法共有1+2+…+9+10+9+…+2+1=100種.
分類標準二:固定和的值.有和為21,22,…,39這幾類,依次有取法10,9,9,8,8, …,2,2,1,1種.由分類計數原理得不同取法共有10+9+9+…+2+2+1+1=100種.
例3 如圖一,要給①,②,③,④四塊區域分別涂上五種顏色中的某一種,允許同一種顏色使用多次,但相鄰區域必須涂不同顏色,則不同涂色方法種數為()
A.
180 B. 
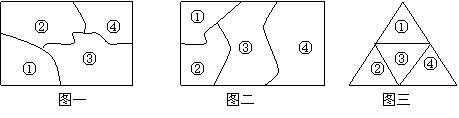
若變為圖二,圖三呢?(240種,5×4×4×4=320種)
例4 如下圖,共有多少個不同的三角形?
解:所有不同的三角形可分為三類”
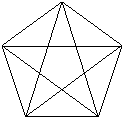 第一類:其中有兩條邊是原五邊形的邊,這樣的三角形共有5個
第一類:其中有兩條邊是原五邊形的邊,這樣的三角形共有5個
第二類:其中有且只有一條邊是原五邊形的邊,這樣的三角形共有5×4=20個
第三類:沒有一條邊是原五邊形的邊,即由五條對角線圍成的三角形,共有5+5=10個
由分類計數原理得,不同的三角形共有5+20+10=35個.
例5 75600有多少個正約數?有多少個奇約數?
解:75600的約數就是能整除75600的整數,所以本題就是分別求能整除75600的整數和奇約數的個數.
由于 75600=24×33×52×7
(1) 75600的每個約數都可以寫成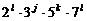 的形式,其中
的形式,其中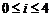 ,
,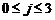 ,
,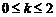 ,
,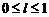
于是,要確定75600的一個約數,可分四步完成,即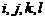 分別在各自的范圍內任取一個值,這樣
分別在各自的范圍內任取一個值,這樣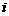 有5種取法,
有5種取法,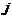 有4種取法,
有4種取法,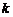 有3種取法,
有3種取法,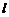 有2種取法,根據分步計數原理得約數的個數為5×4×3×2=120個.
有2種取法,根據分步計數原理得約數的個數為5×4×3×2=120個.
(2)奇約數中步不含有2的因數,因此75600的每個奇約數都可以寫成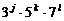 的形式,同上奇約數的個數為4×3×2=24個.
的形式,同上奇約數的個數為4×3×2=24個.
三、課堂練習:
1.用1,2,3,4,5可組成多少個三位數?(各位上的數字允許重復)
2.用數字1,2,3可寫出多少個小于1000的正整數? (各位上的數字允許重復)
3.集合A={a,b,c,d,e},集合B={1,2,3},問A到B的不同映射f共有多少個?B到A的映射g共有多少個?
4.將3封信投入4個不同的郵筒的投法共有多少種?
5. 4名學生從3個不同的樓梯下樓的方法數.
6. 4名學生分配到3個車間去勞動,共有多少中不同的分配方案?
7. 求集合{1,2,3,4,5}的子集的個數
答案:1. 5×5×5×5=625 2. 3+32+33=39 3. 35,53 4. 43 5. 34 6. 34
7. 在集合{1,2,3,4,5}的子集中,每個元素都只有出現和不出現這2種可能,所以這個集合的子集的個數為2×2×2×2×2=25=32個.
四、小結 :分類計數原理和分步計數原理,回答的都是有關做一件事的不同方法種數的問題,區別在于:分類計數原理針對的是“分類”問題,其中各種方法相互獨立,每一種方法只屬于某一類,用其中任何一種方法都可以做完這件事;分步計數原理針對的是“分步”問題,各個步驟中的方法相互依存,某一步驟中的每一種方法都只能做完這件事的一個步驟,只有各個步驟都完成才算做完這件事  應用兩種原理解題:1.分清要完成的事情是什么;2.是分類完成還是分步完成,“類”間互相獨立,“步”間互相聯系;3.有無特殊條件的限制
應用兩種原理解題:1.分清要完成的事情是什么;2.是分類完成還是分步完成,“類”間互相獨立,“步”間互相聯系;3.有無特殊條件的限制
五、課后作業: 
1.用0,1,2,3,4,5這六個數字,
(1)可以組成多少個數字不重復的三位數?
(2)可以組成多少個數字允許重復的三位數?
(3)可以組成多少個數字不允許重復的三位數的奇數?
(4)可以組成多少個數字不重復的小于1000的自然數?
(5)可以組成多少個大于3000,小于5421的數字不重復的四位數?
解(1)分三步:①先選百位數字.由于0不能作百位數,因此有5種選法;②十位數字有5種選法;
③個位數字有4種選法.由乘法原理知所求不同三位數共有5×5×4=100個.
(2)分三步:(1)百位數字有5種選法;(ii)十位數字有6位選法;(iii)個位數字有6種選法.
所求三位數共有5×6×6=180個.
(3)分三步:①先選個位數字,有3種選法;②再選百位數字,有4種選法;③選十位數字也是4
種選法,所求三位奇數共有3×4×4=48個.
(4)分三類:①一位數,共有6個;②兩位數,共有5×5=25個;③三位數共有5×5×4=100個.
因此,比1000小的自然數共有6+25+100=131個.
(5)分4類:①千位數字為3,4之一時,共有2×5×4×3=120個;②千位數字為5,百位數字為
0,1,2,3之一時,共有4×4×3=48個;③千位數字是5,百位數字是4,十位數字為0,1之一
時,共有2×3=6個;④還有5420也是滿條件的1個.故所求自然數共120+48+6+1=175個.
說明:⑴排數字問題是最常見的一種類型,要特別注意首位不能排0.
⑵第(5)題改成:可以組成多少個大于3000,小于5421的四位數?
答案:2*6*6*6+4*6*6+2*6+1=589個
2.求下列集合的元素個數.
(1)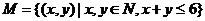 ;
;
(2)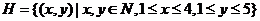 .
.
解:(1)分7類:①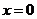 ,
,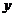 有7種取法;②
有7種取法;②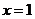 ,
,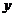 有6種取法; ③
有6種取法; ③ ,
,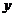 有5種取法; ④
有5種取法; ④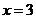 ,
,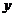 有4種取法; ⑤
有4種取法; ⑤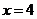 ,
,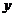 有3種取法; ⑥
有3種取法; ⑥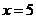 ,
,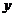 有2種取法;⑦
有2種取法;⑦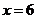 ,
,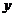 只有1種取法
只有1種取法 因此
因此 共有
共有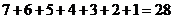 個元素
個元素
(2)分兩步:①先選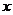 ,有4種可能;②再選
,有4種可能;②再選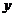 有5種可能.由乘法原理,
有5種可能.由乘法原理,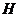 共有
共有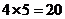 個元素
個元素
3.有四位同學參加三項不同的比賽,
(1)每位同學必須參加一項競賽,有多少種不同的結果?
(2)每項競賽只許一位學生參加,有多少種不同的結果?
解:(1)每位學生有三種選擇,四位學生共有參賽方法: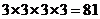 種;
種;
(2)每項競賽被選擇的方法有四種,三項競賽共有參賽方法: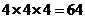 種.
種.
4.①設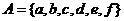 ,
,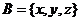 ,從
,從 到
到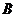 共有多少個不同映射?
共有多少個不同映射?
②6個人分到3個車間,共有多少種分法?
解:(1)分6步:先選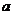 的象,有3種可能,再選
的象,有3種可能,再選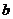 的象也是3種可能,…,選
的象也是3種可能,…,選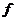 象也有3種可能, 由乘法原理知,共有
象也有3種可能, 由乘法原理知,共有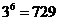 種不同映射;
種不同映射;
(2)把6個人構成的集合,看成上面(1)中之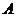 ,3個車間構成的集合,看成上面的
,3個車間構成的集合,看成上面的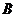 , 因此,所求問題轉化為映射問題,如上題所述,共有
, 因此,所求問題轉化為映射問題,如上題所述,共有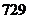 種方案
種方案
5.甲、乙、丙、丁四個人各寫一張賀卡,放在一起,再各取一張不是自己所寫的賀卡,共有多少種不同的取法?
解:列表排出所有的分配方案,共有3+3+3=9種,或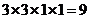 種.
種.
六、板書設計(略) 
七、課后記: 
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com