
2008年遼寧省十二市初中畢業生學業考試
數學試卷(六三制)
一、選擇題(下列各題的備選答案中,只有一個是正確的,請將正確答案的序號填入下面表格內,每小題3分,共24分)
1.截止
A.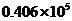 套 B.
套 B.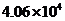 套 C.
套 C.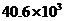 套 D.
套 D.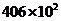 套
套
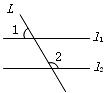
2.如圖,直線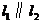 ,
,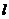 分別與
分別與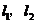 相交,如果
相交,如果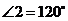 ,那么
,那么 的度數是( )
的度數是( )
A.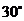 B.
B.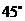 C.
C.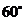 D.
D.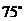
3.下列事件中是必然事件的是( )
A.陰天一定下雨
B.隨機擲一枚質地均勻的硬幣,正面朝上
C.男生的身高一定比女生高
D.將油滴在水中,油會浮在水面上
4.下圖是由幾個相同的小正方體搭成的一個幾何體,它的俯視圖是( )

5.下列命題中正確的是( )
A.兩條對角線互相平分的四邊形是平行四邊形
B.兩條對角線相等的四邊形是矩形
C.兩條對角線互相垂直的四邊形是菱形
D.兩條對角線互相垂直且平分的四邊形是正方形
6.若反比例函數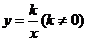 的圖象經過點
的圖象經過點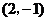 ,則這個函數的圖象一定經過點( )
,則這個函數的圖象一定經過點( )
7.不等式組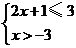 的解集在數軸上表示正確的是( )
的解集在數軸上表示正確的是( )

8.下圖是對稱中心為點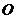 的正八邊形.如果用一個含
的正八邊形.如果用一個含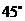 角的直角三角板的角,借助點
角的直角三角板的角,借助點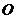 (使角的頂點落在點
(使角的頂點落在點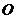 處)把這個正八邊形的面積
處)把這個正八邊形的面積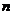 等分.那么
等分.那么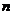 的所有可能的值有( )
的所有可能的值有( )
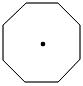
A.2個 B.3個 C.4個 D.5個
二、填空題(每小題3分,共24分)
9.分解因式: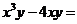 .
.
10.體育老師對甲、乙兩名同學分別進行了8次跳高測試,經計算這兩名同學成績的平均數相同,甲同學的方差是 ,乙同學的方差是
,乙同學的方差是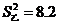 ,那么這兩名同學跳高成績比較穩定的是
同學.
,那么這兩名同學跳高成績比較穩定的是
同學.
11.一元二次方程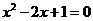 的解是
.
的解是
.
12.如圖,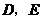 分別是
分別是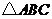 的邊
的邊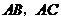 上的點,
上的點,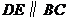 ,
,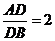 ,則
,則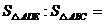 .
.
13.如圖,假設可以在圖中每個小正方形內任意取點(每個小正方形除顏色外完全相同),
那么這個點取在陰影部分的概率是 .

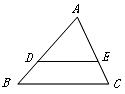
14.一個圓錐底面周長為 cm,母線長為
cm,母線長為
15.如圖,觀察下列圖案,它們都是由邊長為
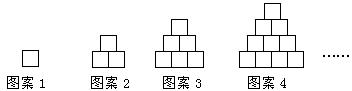
16.如圖,直線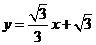 與
與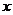 軸、
軸、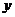 軸分別相交于
軸分別相交于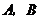 兩點,圓心
兩點,圓心 的坐標為
的坐標為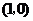 ,⊙
,⊙ 與
與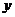 軸相切于點
軸相切于點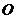 .若將⊙
.若將⊙ 沿
沿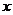 軸向左移動,當⊙
軸向左移動,當⊙ 與該直線相交時,橫坐標為整數的點
與該直線相交時,橫坐標為整數的點 有
個.
有
個.
三、(每小題8分,共16分)
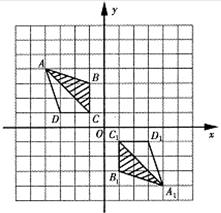
18.如圖所示,在網格中建立了平面直角坐標系,每個小正方形的邊長均為1個單位長度,將四邊形 繞坐標原點
繞坐標原點 按順時針方向旋轉
按順時針方向旋轉 后得到四邊形
后得到四邊形 .
.
(1)直接寫出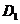 點的坐標;
點的坐標;
(2)將四邊形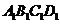 平移,得到四邊形
平移,得到四邊形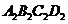 ,若
,若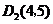 ,畫出平移后的圖形.(友情提示:畫圖時請不要涂錯陰影的位置哦!)
,畫出平移后的圖形.(友情提示:畫圖時請不要涂錯陰影的位置哦!)
四、(每小題10分,共20分)
19.如圖,有四張背面相同的紙牌 ,其正面分別畫有四個不同的圖形,小明將這四張紙牌背面朝上洗勻后隨機摸出一張,放回后洗勻再隨機摸出一張.
,其正面分別畫有四個不同的圖形,小明將這四張紙牌背面朝上洗勻后隨機摸出一張,放回后洗勻再隨機摸出一張.
(1)用樹狀圖(或列表法)表示兩次摸牌所有可能出現的結果(紙牌用 表示);
表示);
(2)求兩次摸牌的牌面圖形既是中心對稱圖形又是軸對稱圖形的概率.

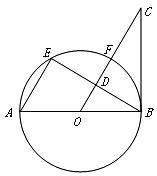
20.如圖, 為⊙
為⊙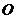 的直徑,
的直徑, 為弦
為弦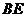 的中點,連接
的中點,連接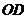 并延長交⊙
并延長交⊙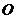 于點
于點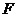 ,與過
,與過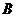 點的切線相交于點
點的切線相交于點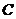 .若點
.若點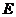 為
為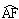 的中點,連接
的中點,連接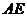 .
.
求證: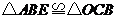 .
.
五、(每小題10分,共20分)
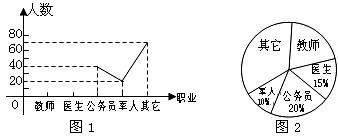
21.某中學開展以“我最喜歡的職業”為主題的調查活動.通過對學生的隨機抽樣調查得到一組數據,下面兩圖(如圖1、圖2)是根據這組數據繪制的兩幅不完整的統計圖.請你根據圖中所提供的信息解答下列問題:
(1)求在這次活動中一共調查了多少名學生?
(2)在扇形統計圖中,求“教師”所在扇形的圓心角的度數.
(3)補全兩幅統計圖.
22.在“汶川地震”捐款活動中,某同學對甲、乙兩班捐款情況進行了統計:甲班捐款人數比乙班捐款人數多3人,甲班共捐款2400元,乙班共捐款1800元,乙班平均每人捐款的錢數是甲班平均每人捐款錢數的 倍.求甲、乙兩班各有多少人捐款?
倍.求甲、乙兩班各有多少人捐款?
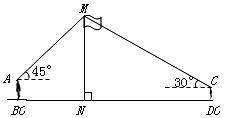
六、(每小題10分,共20分)
23.如圖,某數學興趣小組在活動課上測量學校旗桿高度.已知小明的眼睛與地面的距離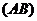 是
是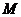 的仰角為
的仰角為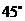 ;小紅的眼睛與地面的距離
;小紅的眼睛與地面的距離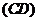 是
是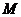 的仰角為
的仰角為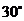 .兩人相距
.兩人相距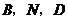 在同一條直線上).
在同一條直線上).
請求出旗桿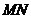 的高度.(參考數據:
的高度.(參考數據: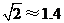 ,
, ,結果保留整數)
,結果保留整數)
24. 兩種款式的布質環保購物袋,每天共生產4500個,兩種購物袋的成本和售價如下表,設每天生產
兩種款式的布質環保購物袋,每天共生產4500個,兩種購物袋的成本和售價如下表,設每天生產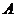 種購物袋
種購物袋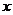 個,每天共獲利
個,每天共獲利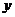 元.
元.
成本(元/個)
售價(元/個)
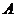
2
2.3
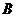
3
3.5
(1)求出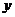 與
與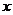 的函數關系式;
的函數關系式;
(2)如果該廠每天最多投入成本10000元,那么每天最多獲利多少元?
七、(本題12分)
25.如圖,在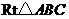 中,
中, ,
,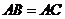 ,
,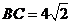 ,另有一等腰梯形
,另有一等腰梯形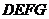 (
(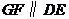 )的底邊
)的底邊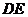 與
與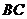 重合,兩腰分別落在
重合,兩腰分別落在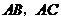 上,且
上,且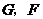 分別是
分別是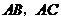 的中點.
的中點.
(1)求等腰梯形 的面積;
的面積;
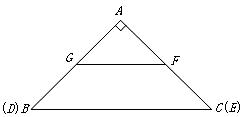
(2)操作:固定 ,將等腰梯形
,將等腰梯形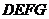 以每秒1個單位的速度沿
以每秒1個單位的速度沿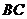 方向向右運動,直到點
方向向右運動,直到點 與點
與點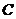 重合時停止.設運動時間為
重合時停止.設運動時間為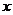 秒,運動后的等腰梯形為
秒,運動后的等腰梯形為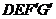 (如圖).
(如圖).
探究1:在運動過程中,四邊形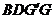 能否是菱形?若能,請求出此時
能否是菱形?若能,請求出此時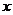 的值;若不能,請說明理由.
的值;若不能,請說明理由.
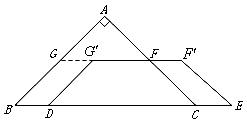
探究2:設在運動過程中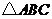 與等腰梯形
與等腰梯形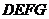 重疊部分的面積為
重疊部分的面積為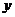 ,求
,求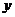 與
與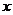 的函數關系式.
的函數關系式.
八、(本題14分)
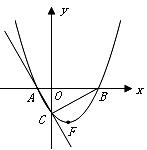
(1)求過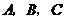 三點拋物線的解析式并求出頂點
三點拋物線的解析式并求出頂點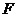 的坐標;
的坐標;
(2)在拋物線上是否存在點 ,使
,使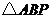 為直角三角形,若存在,直接寫出
為直角三角形,若存在,直接寫出 點坐標;若不存在,請說明理由;
點坐標;若不存在,請說明理由;
(3)試探究在直線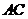 上是否存在一點
上是否存在一點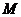 ,使得
,使得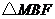 的周長最小,若存在,求出
的周長最小,若存在,求出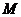 點的坐標;若不存在,請說明理由.
點的坐標;若不存在,請說明理由.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com