
2006年才上海市青浦區初三綜合試卷
一、填空題(本題共12小題,每小題3分,滿分36分)
1、計算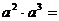 .
.
2、若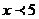 ,則
,則 =
.
=
.
3、因式分解: =
.
=
.
4、函數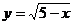 的定義域是
.
的定義域是
.
5、函數 的圖象的兩個分支分別在第二、四象限內,則
的圖象的兩個分支分別在第二、四象限內,則 的取值范圍是
.
的取值范圍是
.
6、當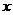 =
時,分式
=
時,分式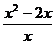 的值為零.
的值為零.
7、方程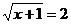 的解是
.
的解是
.
8、為了解決藥品價格過高的問題,本市決定大幅度降低藥品價格,其中將原價為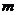 元的某種常用藥降價20%,則降價后此藥價格為
.
元的某種常用藥降價20%,則降價后此藥價格為
.
9、梯形的中位線長為4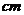 ,高為6
,高為6 ,則該梯形的面積為
.
,則該梯形的面積為
.
10、已知兩個相似三角形的周長比是1:3 ,則它們的面積比是 .
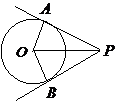 11、如圖,
11、如圖,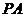 、
、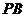 是⊙
是⊙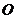 的兩條切線,切點是
的兩條切線,切點是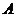 、
、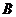 ,
,
如果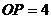 ,
,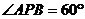 ,那么⊙
,那么⊙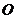 的半徑是
.
的半徑是
.
 12、如圖,把一個直角三角形
12、如圖,把一個直角三角形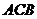 繞著
繞著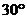 角的頂點
角的頂點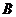
順時針旋轉,使點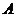 與
與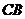 的延長線上的點E重合,
的延長線上的點E重合,
這時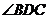 的度數是
.
的度數是
.
[本題每小題所列出的四個選項中,只有一個是正確的,把正確答案的代號填入括號內]
二、選擇題(本大題共4題,每小題4分,滿分16分)
13、下列說法正確的是……………………………………………………………… ( )
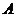 )
) 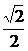 是分數
是分數
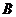 )實數
)實數 的倒數是
的倒數是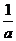
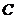 ) 負數沒有平方根
) 負數沒有平方根
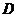 )絕對值等于本身的數是正數
)絕對值等于本身的數是正數
14、將二次函數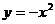 的圖象向右平移3個單位,再向上平移2個單位,那么所得的二次
的圖象向右平移3個單位,再向上平移2個單位,那么所得的二次
函數解析式為…………………………………………………………………… ( )
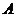 )
)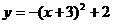
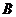 )
)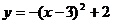
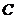 )
)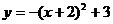
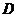 )
)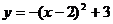
15、如圖,已知四邊形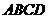 是平行四邊形,下列結論中,不正確的是…… ( )
是平行四邊形,下列結論中,不正確的是…… ( )

 )當
)當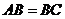 時,它是菱形
時,它是菱形
 )當
)當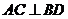 時,它是菱形
時,它是菱形
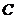 )當
)當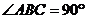 時,它是矩形
時,它是矩形
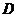 ) 當
) 當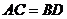 時,它是等腰梯形
時,它是等腰梯形
16、已知⊙ 和⊙
和⊙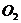 的半徑分別為4
的半徑分別為4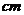 和
和 ,圓心距
,圓心距
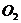 =5
=5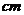 ,則⊙
,則⊙ 與⊙
與⊙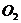
的公切線的條數為…………………………………………………………… ( )
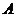 ) 1條
) 1條
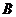 ) 2條
) 2條 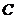 ) 3條
) 3條
 ) 4條
) 4條
三、(本大題共5題,第17、18題每題9分,第19~21題每題10分,滿分48分)
17、已知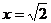 ,求
,求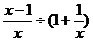 的值.
的值.
18、已知方程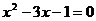 的兩根為
的兩根為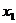 、
、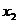 ,求
,求 的值.
的值.
19、解方程組:
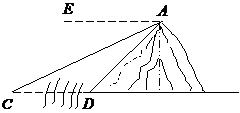 20、如圖,河旁有一座小山,從山頂
20、如圖,河旁有一座小山,從山頂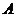 處測得河對岸點
處測得河對岸點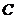 的俯角為
的俯角為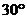 ,測得岸邊點
,測得岸邊點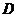 的俯角為
的俯角為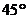 ,現從山頂
,現從山頂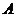 到河對岸點
到河對岸點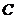 拉一條筆直的纜繩
拉一條筆直的纜繩 ,如果
,如果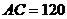 米,求河寬
米,求河寬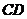 的長.
的長.
 21、如圖,矩形
21、如圖,矩形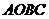 ,以
,以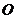 為坐標原點,
為坐標原點,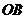 、
、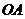 分別在
分別在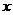 軸、
軸、 軸上,點
軸上,點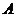 的坐標為(0,3),點
的坐標為(0,3),點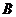 的坐標為(5,0),點
的坐標為(5,0),點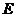 是
是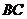 邊上一點,如把矩形
邊上一點,如把矩形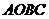 沿
沿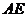 翻折后,
翻折后,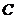 點恰好落在
點恰好落在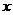 軸上點
軸上點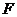 處.
處.
(1)求點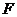 的坐標;
的坐標;
(2)求線段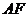 所在直線的解析式.
所在直線的解析式.
四、(本大題共4題,第22、23、24題每題12分,第25題14分,滿分50分)
22、為了迎接初三數學學業考試,這學期共進行了10次數學專題測驗,其中小麗的數學專題測驗成績情況如圖所示:
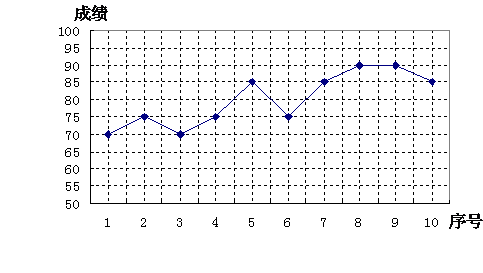
利用圖中提供的信息,解答下列問題:
(1)小麗這10次數學專題測驗成績的平均數為 、中位數為 、方差為 ;
(2)如果將90分以上(含90分)成績視為優秀,則小麗這10次數學專題測驗成績的優秀
率是 ;
(3)根據以上信息,請你對小麗同學提一條學習建議.
23、如圖,已知⊙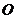 的弦
的弦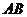 垂直于直徑
垂直于直徑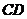 ,垂足為
,垂足為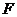 ,連接
,連接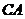 、
、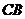 .
.
 (1)求證:
(1)求證: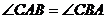 ;
;
(2)在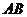 上有一點
上有一點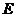 ,延長
,延長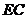 到點
到點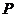 ,連接
,連接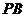 ,
,
若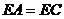 ,
,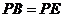 ,求證:
,求證: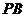 是⊙
是⊙ 的切線.
的切線.
24、如圖,已知二次函數 的圖象經過點
的圖象經過點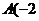 ,
,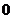 )、
)、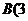 ,
,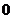 ),與
),與 軸交
軸交
 于點
于點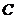 .
.
(1)求該二次函數的解析式;
(2)如在線段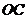 上有一點
上有一點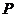 ,且點
,且點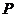 到點
到點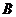 的
的
距離為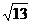 ,那么在
,那么在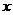 軸上是否存在點
軸上是否存在點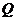 ,
,
使以點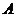 、
、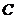 、
、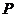 、
、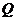 為頂點的四邊形是梯
為頂點的四邊形是梯
形?如存在,請求出點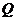 的坐標;如不存在,
的坐標;如不存在,
請說明理由.
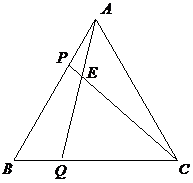
25、如圖,等邊三角形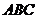 的邊長為3,點
的邊長為3,點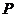 、
、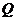 分別是
分別是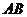 、
、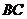 上的動點(點
上的動點(點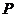 、
、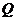
與三角形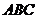 的頂點不重合),且
的頂點不重合),且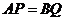 ,
, 、
、 相交于點
相交于點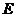 .
.
(1)如設線段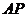 為
為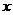 ,線段
,線段 為
為 ,求
,求 關于
關于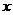 的函數解析式,并寫出定義域;
的函數解析式,并寫出定義域;
(2)當△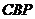 的面積是△
的面積是△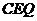 的面積的2倍時,求
的面積的2倍時,求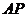 的長;
的長;
(3)點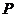 、
、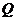 分別在
分別在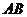 、
、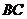 上移動過程中,
上移動過程中, 和
和 能否互相垂直?如能,請指
能否互相垂直?如能,請指
 出
出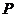 點的位置;如不能,請說明理由.
點的位置;如不能,請說明理由.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com