Question

1．已知當x∈R，[x]表示不超過x的最大整數，稱y=[x]為取整函數，例如[1.2]=1，[-2.3]=-3，若f（x）=[x]，且偶函數g（x）=-（x-1）²+1（x≥0），則方程f（f（x））=g（x）的所有解之和為（　　）

• A． 1
• B． -2
• C． $\sqrt{5}-3$
• D． $-\sqrt{5}-3$

Answer 1

分析 由偶函數的性質和條件求出x＜0時對應的g（x），由[x]的意義和偶函數的圖象性質，在同一個坐標系中畫出f（f（x））和g（x）的函數圖象，根據圖象分別求出交點的縱坐標，代入g（x）的解析式求對應的橫坐標，即可得到答案．

解答 解：設x＜0，則-x＞0，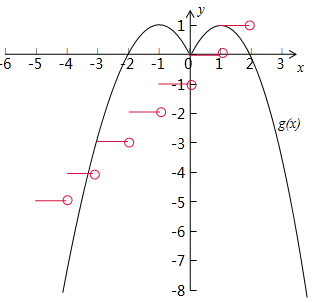
∵偶函數g（x）=-（x-1）²+1（x≥0），
∴g（x）=g（-x）=-（-x-1）²+1=-（x+1）²+1，
由f（x）=[x]得，f（f（x））=[x]，
在同一個坐標系中畫出f（f（x））和g（x）的函數圖象，如圖所示：
由圖可得，兩個圖象有四個交點，交點的縱坐標分為1、0、-3、-4，
當x≥0時，方程f（f（x））=g（x）的解是0和1；
當x＜0時，
令g（x）=-（x+1）²+1=-3，解得x=-3，
令g（x）=-（x+1）²+1=-4，解得x=-1-$\sqrt{5}$，
綜上得，f（f（x））=g（x）的解是：
0、1、-3、-1-$\sqrt{5}$，
所有解之和是$-3-\sqrt{5}$，
故選：D．

點評 本題考查函數奇偶性的圖象與性質，取整函數的圖象，以及方程根的轉化，考查數形結合思想，轉化思想，分析問題、解決問題的能力．