
| A. | -2 | B. | 2 | C. | $-\frac{2}{3}$ | D. | $\frac{2}{3}$ |
分析 根據題意,由f(x-2)=f(x+2),分析可得f(x)=f(x+4),即可得函數f(x)的周期為4,則有f(9)=f(1),由函數的解析式以及奇偶性可得f(1)的值,即可得答案.
解答 解:根據題意,函數f(x)滿足f(x-2)=f(x+2),即f(x)=f(x+4),
則函數f(x)的周期為4,
f(9)=f(1),
又由函數f(x)為奇函數,則f(1)=-f(-1),
又由當x∈[-2,0]時,f(x)=3x-1,
則f(-1)=3-1-1=$\frac{1}{3}$-1=-$\frac{2}{3}$;
則有f(9)=f(1)=-f(-1)=$\frac{2}{3}$;
故選:D.
點評 本題考查函數奇偶性、周期性的應用,注意分析得到函數的周期.


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案 暑假接力賽新疆青少年出版社系列答案
暑假接力賽新疆青少年出版社系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{10}$ | D. | $\frac{9}{10}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $m≥\frac{1}{e}$ | B. | $0<m≤\frac{1}{e}$ | C. | $m≥\frac{1}{e^2}$ | D. | $0<m≤\frac{1}{e^2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 10 | B. | -10 | C. | 20 | D. | -20 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
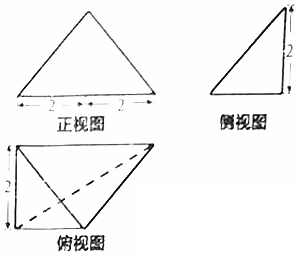
| A. | $6+4\sqrt{2}+2\sqrt{6}$ | B. | $4+6\sqrt{2}+2\sqrt{5}$ | C. | $4+2\sqrt{5}+2\sqrt{6}$ | D. | $4+6\sqrt{2}+2\sqrt{6}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com