
分析 由約束條件作出可行域,化目標函數為直線方程的斜截式,數形結合得到最優解,聯立方程組求出最優解的坐標,代入目標函數得答案.
解答 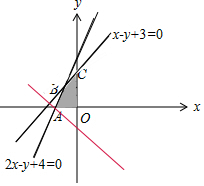 解:由實數x,y滿足$\left\{\begin{array}{l}{2x-y+4≥0}\\{x-y+3≥0}\\{x≤0}\\{y≥0}\end{array}\right.$,作出可行域如圖,
解:由實數x,y滿足$\left\{\begin{array}{l}{2x-y+4≥0}\\{x-y+3≥0}\\{x≤0}\\{y≥0}\end{array}\right.$,作出可行域如圖,
化目標函數z=-3y-2x為y=$-\frac{2}{3}$x-$\frac{z}{3}$,
由圖可知,當直線y=$-\frac{2}{3}$x-$\frac{z}{3}$過A(-2,0)時,直線在y軸上的截距最小,z有最大值,等于-3×0+2×2=4.
故答案為:4.
點評 本題考查了簡單的線性規劃,考查了數形結合的解題思想方法,是中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | -9 | B. | 9 | C. | 10 | D. | 0 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
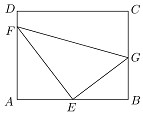 如圖,某污水處理廠要在一個矩形ABCD的池底水平鋪設污水凈化管道(直角△EFG,E是直角頂點)來處理污水,管道越長,污水凈化效果越好,設計要求管道的接口E是AB的中點,F、G分別落在AD、BC上,且AB=20m,$AD=10\sqrt{3}m$,設∠GEB=θ.
如圖,某污水處理廠要在一個矩形ABCD的池底水平鋪設污水凈化管道(直角△EFG,E是直角頂點)來處理污水,管道越長,污水凈化效果越好,設計要求管道的接口E是AB的中點,F、G分別落在AD、BC上,且AB=20m,$AD=10\sqrt{3}m$,設∠GEB=θ.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -2 | B. | 2 | C. | $-\frac{2}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $[-\frac{3}{4}π,\frac{π}{4}]$ | B. | [-π,0] | C. | $[-\frac{π}{4},\frac{3}{4}π]$ | D. | $[-\frac{π}{2},\frac{π}{2}]$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com