
分析 (1)先用數學歸納法證明1<an<2.由.${a_{n+1}}-{a_n}=a_n^2-3{a_n}+2=({{a_n}-1})({{a_n}-2})<0$.
可證得1<an+1<an<2成立.
(2)${a_1}=\frac{3}{2}=\frac{6}{{3+{2^{1-1}}}},{a_2}=\frac{5}{4}>\frac{6}{{3+{2^{2-1}}}}$,
當n≥3時,由${a_{n+1}}=a_n^2-2{a_n}+2$,得$2-{a_{n+1}}=2{a_n}-a_n^2$,
$⇒\frac{1}{{2-{a_{n+1}}}}=\frac{1}{2}({\frac{1}{{2-{a_n}}}+\frac{1}{a_n}})<\frac{1}{2}({\frac{1}{{2-{a_n}}}+1})$,$⇒\frac{1}{{2-{a_{n+1}}}}-1<\frac{1}{2}({\frac{1}{{2-{a_n}}}-1})$
$⇒\frac{1}{{2-{a_n}}}-1<\frac{1}{{{2^{n-1}}}}({\frac{1}{{2-{a_1}}}-1})=\frac{1}{{{2^{n-1}}}}$$⇒{a_n}≤\frac{{{2^{n-1}}+2}}{{{2^{n-1}}+1}}$
即可證得$\frac{6}{{{2^{n-1}}+3}}≤{a_n}≤\frac{{{2^{n-1}}+2}}{{{2^{n-1}}+1}}$
(3)由(1)1<an<2得sn>n
由(2)得${a_n}≤\frac{{{2^{n-1}}+2}}{{{2^{n-1}}+1}}=1+\frac{1}{{{2^{n-1}}+1}}<1+\frac{1}{{{2^{n-1}}}}$,
${s_n}<({1+\frac{1}{{{2^{1-1}}}}})+({1+\frac{1}{{{2^{2-1}}}}})+…+({1+\frac{1}{{{2^{n-1}}}}})=n+\frac{{1-\frac{1}{2^n}}}{{1-\frac{1}{2}}}=n+2({1-\frac{1}{2^n}})<n+2$
解答 證明:(1)先用數學歸納法證明1<an<2.
①.n=1時$1<{a_1}=\frac{3}{2}<2$,
②.假設n=k時成立,即1<ak<2.
那么n=k+1時,${a_{k+1}}=a_k^2-2{a_k}+2∈({1,2}),{a_k}∈({1,2})$成立.
由①②知1<an<2,n∈N*恒成立.${a_{n+1}}-{a_n}=a_n^2-3{a_n}+2=({{a_n}-1})({{a_n}-2})<0$.
所以1<an+1<an<2成立.
(2)${a_1}=\frac{3}{2}=\frac{6}{{3+{2^{1-1}}}},{a_2}=\frac{5}{4}>\frac{6}{{3+{2^{2-1}}}}$,
當n≥3時,$\frac{6}{{{2^{n-1}}+3}}<1$而1<an<2.所以${a_n}≥\frac{6}{{{2^{n-1}}+3}}$.
由${a_{n+1}}=a_n^2-2{a_n}+2$,得$2-{a_{n+1}}=2{a_n}-a_n^2$,
$⇒\frac{1}{{2-{a_{n+1}}}}=\frac{1}{2}({\frac{1}{{2-{a_n}}}+\frac{1}{a_n}})<\frac{1}{2}({\frac{1}{{2-{a_n}}}+1})$
$⇒\frac{1}{{2-{a_{n+1}}}}-1<\frac{1}{2}({\frac{1}{{2-{a_n}}}-1})$
$⇒\frac{1}{{2-{a_n}}}-1<\frac{1}{{{2^{n-1}}}}({\frac{1}{{2-{a_1}}}-1})=\frac{1}{{{2^{n-1}}}}$$⇒{a_n}≤\frac{{{2^{n-1}}+2}}{{{2^{n-1}}+1}}$
所以$\frac{6}{{{2^{n-1}}+3}}≤{a_n}≤\frac{{{2^{n-1}}+2}}{{{2^{n-1}}+1}}$
(3)由(1)1<an<2得sn>n
由(2)得${a_n}≤\frac{{{2^{n-1}}+2}}{{{2^{n-1}}+1}}=1+\frac{1}{{{2^{n-1}}+1}}<1+\frac{1}{{{2^{n-1}}}}$,
${s_n}<({1+\frac{1}{{{2^{1-1}}}}})+({1+\frac{1}{{{2^{2-1}}}}})+…+({1+\frac{1}{{{2^{n-1}}}}})=n+\frac{{1-\frac{1}{2^n}}}{{1-\frac{1}{2}}}=n+2({1-\frac{1}{2^n}})<n+2$
點評 本題考查了數列遞推式,數學歸納法,及數列與不等式,屬于難題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
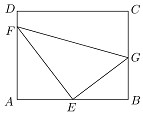 如圖,某污水處理廠要在一個矩形ABCD的池底水平鋪設污水凈化管道(直角△EFG,E是直角頂點)來處理污水,管道越長,污水凈化效果越好,設計要求管道的接口E是AB的中點,F、G分別落在AD、BC上,且AB=20m,$AD=10\sqrt{3}m$,設∠GEB=θ.
如圖,某污水處理廠要在一個矩形ABCD的池底水平鋪設污水凈化管道(直角△EFG,E是直角頂點)來處理污水,管道越長,污水凈化效果越好,設計要求管道的接口E是AB的中點,F、G分別落在AD、BC上,且AB=20m,$AD=10\sqrt{3}m$,設∠GEB=θ.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -2 | B. | 2 | C. | $-\frac{2}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,1) | B. | (0,1] | C. | (1,2) | D. | (1,2] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-2,+∞) | B. | [-2,+∞) | C. | (-∞,-2) | D. | (-∞,-2] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
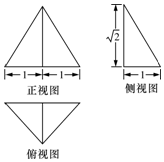
| A. | 外接球的體積為12$\sqrt{3}$ π | B. | 外接球的表面積為4π | ||
| C. | 體積為$\sqrt{2}$ | D. | 表面積為$\sqrt{5}$+$\sqrt{2}$+1 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com