一区二区三区四区在线视频,中国妞xxxhd露脸偷拍视频,一本一道久久精品综合

9．將下列角度化為弧度，弧度轉化為角度
（1）780°，（2）-1560°，（3）67.5°（4）$-\frac{10}{3}π$，（5）$\frac{π}{12}$，（6）$\frac{7π}{4}$．

分析利用π弧度=180^°即可得出．

解答解：（1）780°=$\frac{780}{180}×π$弧度=$\frac{13π}{3}$弧度，
（2）-1560°=-$\frac{1560}{180}×π$弧度=-$\frac{26}{3}$π弧度，
（3）67.5°=$\frac{67.5}{180}π$弧度=$\frac{3π}{8}$弧度．
（4）$-\frac{10}{3}π$弧度=-$\frac{10}{3}×18{0}^{°}$=-600^°，
（5）$\frac{π}{12}$弧度=$\frac{18{0}^{°}}{12}$=15^°，
（6）$\frac{7π}{4}$弧度=$\frac{7}{4}×18{0}^{°}$=315^°．

點評本題考查了弧度與角度的換算關系，考查了推理能力與計算能力，屬于基礎題．

練習冊系列答案

68所名校圖書小升初高分奪冠真卷系列答案

伴你成長周周練月月測系列答案

小升初金卷導練系列答案

萌齊小升初強化模擬訓練系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：選擇題

15．

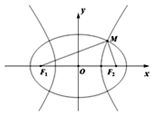已知橢圓C₁：$\frac{{x}^{2}}{{m}^{2}}$+$\frac{{y}^{2}}{{p}^{2}}$=1（m＞p＞0）與雙曲線C₂：$\frac{{x}^{2}}{{n}^{2}}$-$\frac{{y}^{2}}{{p}^{2}}$=1（n＞0）有公共的焦點F₁，F₂，設M為C₁與C₂在第一象限內的交點，|F₁F₂|=2c．則（　　）

	A．	m²+n²=2c²，且∠F₁MF₂＞$\frac{π}{2}$		B．	m²+n²=2c²，且∠F₁MF₂=$\frac{π}{2}$
	C．	m²+n²=4c²，且∠F₁MF₂＞$\frac{π}{2}$		D．	m²+n²=4c²，且∠F₁MF₂=$\frac{π}{2}$

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

16．設函數f（x）=|x-$\frac{4}{m}$|+|x+m|，（m＞0）
（I）證明：f（x）≥4
（II）若f（1）＞5，求m的取值范圍．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

13．2017年春晚過后，為了研究演員上春晚次數與受關注度的關系，某網站對其中一位經常上春晚的演員上春晚次數與受關注度進行了統計，得到如下數據：

上春晚次數x（單位：次）	2	4	6	8	10
粉絲數量y（單位：萬人）	10	20	40	80	100

（1）若該演員的粉絲數量g（x）≤g（1）=0與上春晚次數x滿足線性回歸方程，試求回歸方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$，并就此分析，該演員上春晚12次時的粉絲數量；
（2）若用$\frac{{y}_{i}}{{x}_{i}}$（i=1，2，3，4，5）表示統計數據時粉絲的“即時均值”（四舍五入，精確到整數），從這5個“即時均值”中任選2數，記所選的2數之和為隨機變量η，求η的分布列與數學期望．
參考公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$．

查看答案和解析>>

科目：高中數學 來源： 題型：填空題

4．（x²-$\sqrt{\frac{2}{x}}$）⁵的展開式中常數項為20．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

14．已知極點為直角坐標系的原點，極軸為x軸正半軸且單位長度相同的極坐標系中曲線C₁：ρ=1，${C_2}：\left\{\begin{array}{l}x=\frac{{\sqrt{2}}}{2}t-1\\ y=\frac{{\sqrt{2}}}{2}t+1\end{array}\right.$（t為參數）．
（Ⅰ）求曲線C₁上的點到曲線C₂距離的最小值；
（Ⅱ）若把C₁上各點的橫坐標都擴大為原來的2倍，縱坐標擴大為原來的$\sqrt{3}$倍，得到曲線${C_1}^′$．設P（-1，1），曲線C₂與${C_1}^′$交于A，B兩點，求|PA|+|PB|．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

1．極坐標系中橢圓C的方程為ρ²=$\frac{2}{co{s}^{2}θ+2si{n}^{2}θ}$，以極點為原點，極軸為x軸非負半軸，建立平面直角坐標系，且兩坐標系取相同的單位長度．
（1）若橢圓上任一點坐標為P（x，y），求${x^2}+\sqrt{2}xy$的取值范圍；
（2）若橢圓的兩條弦AB，CD交于點Q，且直線AB與CD的傾斜角互補，求證：|QA|•|QB|=|QC|•|QD|．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

18．下表是某位理科學生連續5次月考的物理、數學的成績，結果如下：

次數	1	2	3	4	5
物理（x分）	90	85	74	68	63
數學（y分）	130	125	110	95	90

（Ⅰ）求該生5次月考物理成績的平均分和方差；
（Ⅱ）一般來說，學生的數學成績與物理成績有較強的線性相關關系，根據上表提供的數據，求兩個變量x，y的線性回歸方程．（小數點后保留一位有效數字）
參考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$，$\overline{x}$，$\overline{y}$表示樣本均值
參考數據：90²+85²+74²+68²+63²=29394，
90×130×85×125×74×110×68×95+63×90=42595．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

19．

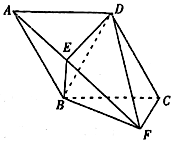如圖，平面ABCD⊥平面BCF，四邊形ABCD是菱形，∠BCF=90°．
（1）求證：BF=DF；
（2）若點E為AF的中點，∠BCD=60°，且BC=CF=2，求四面體BDEF的體積．

查看答案和解析>>

同步練習冊答案

日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

練習冊

高中

初中

小學