
分析 (1)求出函數的導數,解關于導函數的不等式,求出函數的單調區間即可;
(2)求出函數g(x)的二階導數,問題轉化為a≥$\frac{1}{{2e}^{4}}$-$\frac{1}{2}$(x+3)ex,令h(x)=$\frac{1}{{2e}^{4}}$-$\frac{1}{2}$(x+3)ex,根據函數的單調性求出a的范圍即可.
解答 解:(1)f′(x)=ex-$\frac{1}{{(x+1)}^{2}}$,
令f′(x)=0,解得:x=0,
設r(x)=ex-$\frac{1}{{(x+1)}^{2}}$,則r′(x)=ex+$\frac{2}{{(x+1)}^{3}}$,
當x>-1時,r′(x)>0,r(x)在(-1,+∞)上是單調增函數,
故x=0是r(x)在(-1,+∞)內的唯一零點,
即x=0是f′(x)在(-1,+∞)內的唯一零點,
所以當-1<x<0時,f′(x)<0,即f(x)在(-1,0)上是單調減函數;
當x>0時,f′(x)>0,即f(x)在(0,+∞)上是單調增函數.
(II)g(x)=(x+1)[f(x)+1]+(a-$\frac{1}{{2e}^{4}}$)x2=(x+1)ex+(a-$\frac{1}{{2e}^{4}}$)x2+ax,
g′(x)=(x+2)ex+2(a-$\frac{1}{{2e}^{4}}$)x+a,g″(x)=(x+3)ex+2(a-$\frac{1}{{2e}^{4}}$),
如果g(x)在(-∞,-1)是凸函數,那么?x∈(-∞,-1)都有g″(x)≥0,
g″(x)≥0⇒a≥$\frac{1}{{2e}^{4}}$-$\frac{1}{2}$(x+3)ex,
令h(x)=$\frac{1}{{2e}^{4}}$-$\frac{1}{2}$(x+3)ex,即得h′(x)=-$\frac{1}{2}$(x+4)ex,
h′(x)=0⇒x=-4,當x<-4時,h′(x)>0,當-4<x<-1時,h′(x)<0,
即h(x)在(-∞,-4)單調遞增,在(-4,-1)單調遞減,所以h(x)≤h(-4)=e-4,
即a≥e-4,又g(x)在(-∞,-1)不是凸函數,
所以a∈(-∞,e-4).
點評 本題考查了函數的單調性、函數恒成立問題,考查導數的應用以及轉化思想,是一道中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
| 組別 | 理科 | 文科 | ||
| 性別 | 男生 | 女生 | 男生 | 女生 |
| 人數 | 3 | 3 | 3 | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{2}$ | B. | $\frac{3}{2}$ | C. | 2$\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖所示,已知二面角α-l-β的平面角為θ,PA⊥α,PB⊥β,A、B為垂足,且PA=4,PB=5,設A、B到棱l的距離分別為x、y,當θ變化時,點(x,y)的軌跡是下列圖形中的( )
如圖所示,已知二面角α-l-β的平面角為θ,PA⊥α,PB⊥β,A、B為垂足,且PA=4,PB=5,設A、B到棱l的距離分別為x、y,當θ變化時,點(x,y)的軌跡是下列圖形中的( )| A. |  | B. |  | C. | 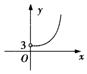 | D. |  |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com