
 如圖所示,已知二面角α-l-β的平面角為θ,PA⊥α,PB⊥β,A、B為垂足,且PA=4,PB=5,設A、B到棱l的距離分別為x、y,當θ變化時,點(x,y)的軌跡是下列圖形中的( )
如圖所示,已知二面角α-l-β的平面角為θ,PA⊥α,PB⊥β,A、B為垂足,且PA=4,PB=5,設A、B到棱l的距離分別為x、y,當θ變化時,點(x,y)的軌跡是下列圖形中的( )| A. |  | B. |  | C. | 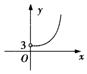 | D. |  |
分析 在平面α內過A作AM⊥l,垂足為M,連結BM,分別在Rt△PAM和Rt△PBM中使用勾股定理計算PM即可得出軌跡方程.
解答  解:在平面α內過A作AM⊥l,垂足為M,連結BM,
解:在平面α內過A作AM⊥l,垂足為M,連結BM,
∵PA⊥α,AM?α,∴PA⊥AM,
∴PM=$\sqrt{P{A}^{2}+A{M}^{2}}$=$\sqrt{16+{x}^{2}}$,
同理PM=$\sqrt{P{B}^{2}+B{M}^{2}}$=$\sqrt{25+{y}^{2}}$,
∴16+x2=25+y2,即x2-y2=9,
又x≥0,y≥0,
∴(x,y)的軌跡是雙曲線$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{9}=1$在第一象限內的部分.
故選:D.
點評 本題考查了線面垂直的性質,屬于基礎題.


科目:高中數學 來源: 題型:選擇題
| A. | ${a_n}=\frac{1}{n}$ | B. | ${a_n}=\frac{1}{n+1}$ | C. | an=n | D. | ${a_{n+1}}=\frac{1}{n}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 4 | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 某大學高等數學這學期分別用A,B兩種不同的數學方式試驗甲、乙兩個大一新班(人數均為60人,入學數學平均分和優秀率都相同;勤奮程度和自覺性都一樣).現隨機抽取甲、乙兩班各20名的高等數學期末考試成績,得到莖葉圖:
某大學高等數學這學期分別用A,B兩種不同的數學方式試驗甲、乙兩個大一新班(人數均為60人,入學數學平均分和優秀率都相同;勤奮程度和自覺性都一樣).現隨機抽取甲、乙兩班各20名的高等數學期末考試成績,得到莖葉圖:| 甲班 | 乙班 | 合計 | |
| 優秀 | |||
| 不優秀 | |||
| 合計 |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,0) | B. | (0,2) | C. | (2,+∞) | D. | (-∞,0)∪(2,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-1)∪(1,+∞) | B. | (-1,1) | C. | (-1,+∞) | D. | (1,+∞) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com