Question

2．過拋物線C：y²=4x的焦點F的直線交拋物線C于A，B兩點，過B與x軸平行的直線和過F與AB垂直的直線交于點N，AN與x軸交于點M，則M的橫坐標的取值范圍為（　　）

• A． （-∞，0）
• B． （0，2）
• C． （2，+∞）
• D． （-∞，0）∪（2，+∞）

Answer 1

分析 設出直線AF的方程，與拋物線聯立，求出B的坐標，求出直線AB，FN的斜率，從而求出直線BN的方程，根據A、M、N三點共線，可求出M的橫坐標的表達式，從而求出m的取值范圍．

解答 解：拋物線方程為y²=4x，F（1，0），可設A（t²，2t），t≠0，t≠±1，
∵AF不垂直y軸，
∴設直線AF：x=sy+1（s≠0），
聯立$\left\{\begin{array}{l}{{y}^{2}=4x}\\{x=sy+1}\end{array}\right.$，得y²-4sy-4=0．
y₁y₂=-4，
∴B（$\frac{1}{{t}^{2}}$，-$\frac{2}{t}$），
又直線AB的斜率為$\frac{2t}{{t}^{2}-1}$，故直線FN的斜率為$\frac{{t}^{2}-1}{2t}$，
從而得FN：y=-$\frac{{t}^{2}-1}{2t}$（x-1），直線BN：y=-$\frac{2}{t}$，
則N（$\frac{{t}^{2}+3}{{t}^{2}-1}$，-$\frac{2}{t}$），
設M（m，0），由A、M、N三點共線，得$\frac{2t}{{t}^{2}-m}$=$\frac{2t+\frac{2}{t}}{{t}^{2}-\frac{{t}^{2}+3}{{t}^{2}-1}}$，
于是m=$\frac{2{t}^{2}}{{t}^{2}-1}$=$\frac{2}{1-\frac{1}{{t}^{2}}}$，得m＜0或m＞2．
經檢驗，m＜0或m＞2滿足題意．
∴點M的橫坐標的取值范圍為（-∞，0）∪（2，+∞）．
故選D．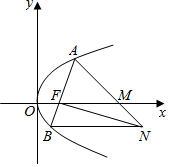

點評 本題考查拋物線的簡單性質，考查直線與圓錐曲線位置關系的應用，考查數學轉化思想方法，屬中檔題．