
分析 (1)取BD中點O,連結BG、OG、MG,利用數形結合思想和空間向量加法法則能化簡$\overrightarrow{AB}+\frac{1}{2}(\overrightarrow{BD}+\overrightarrow{BC})$.
(2)取AB中點E,AC中點F,連結AM、EM、FM、MD,利用數形結合思想和空間向量加法法則能化簡$\overrightarrow{AD}-\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$.
解答 解:(1)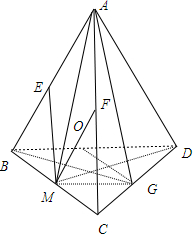 取BD中點O,連結BG、OG、MG,
取BD中點O,連結BG、OG、MG,
∵空間四邊形ABCD,連接AC,BD,設M,G分別是BC,CD的中點,
∴$\overrightarrow{AB}+\frac{1}{2}(\overrightarrow{BD}+\overrightarrow{BC})$
=$\overrightarrow{AB}$+($\overrightarrow{BO}$+$\overrightarrow{BM}$)
=$\overrightarrow{AB}$+$\overrightarrow{BG}$
=$\overrightarrow{AG}$.
(2)取AB中點E,AC中點F,連結AM、EM、FM、MD,
則$\overrightarrow{AD}-\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$
=$\overrightarrow{AD}$=($\overrightarrow{AE}+\overrightarrow{AF}$)
=$\overrightarrow{AD}-\overrightarrow{AM}$
=$\overrightarrow{MD}$.
點評 本題考查向量的化簡,是基礎題,解題時要認真審題,注意數形結合思想和空間向量加法法則的合理運用.


科目:高中數學 來源: 題型:解答題
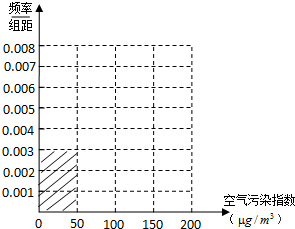
| 空氣污染指數 (單位:μg/m3) | (0,50] | (50,100] | (100,150] | (150,200] |
| 監測點個數 | 15 | 40 | y | 10 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {1,2,3,4} | B. | {2,3,4} | C. | {3,4} | D. | {x|1<x≤4} |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 有最大值$\frac{1}{2}$ | B. | 有最小值$\frac{1}{2}$ | C. | 有最大值$\frac{1}{4}$ | D. | 有最小值$\frac{1}{4}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com