
分析 由已知得|$\overrightarrow{AP}$|2=(x$\overrightarrow{AB}$+y$\overrightarrow{AD}$)2=9x2+4y2≥(3x+2y)2-$\frac{1}{2}$(3x+2y)2=$\frac{1}{2}$(3x+2y)2,從而得到3x+2y≤$\sqrt{2}$,以A為原點,AB為x軸,AD為y軸,建立平面直角坐標系,則$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$=(3x,2y),從而3x+2y>1,由此能求出3x+2y的取值范圍.
解答 解:∵矩形ABCD中,AB=3,AD=2,P矩形內部一點,且AP=1,$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,
∴|$\overrightarrow{AP}$|2=(x$\overrightarrow{AB}$+y$\overrightarrow{AD}$)2=9x2+4y2
=(3x+2y)2-12xy≥(3x+2y)2-$\frac{1}{2}$(3x+2y)2
=$\frac{1}{2}$(3x+2y)2
∵|$\overrightarrow{AP}$|2=1,∴$\frac{1}{2}$(3x+2y)2≤1,故3x+2y≤$\sqrt{2}$,
如圖,以A為原點,AB為x軸,AD為y軸,建立平面直角坐標系,
則A(0,0),B(3,0),D(0,2),
∴$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$=x(3,0)+y(0,2)=(3x,2y),
∴由三角形中兩邊和大于第三邊,得:3x+2y>1,
∴3x+2y的取值范圍是(1,$\sqrt{2}$].
故答案為:$({1,\sqrt{2}}]$.
點評 本題考查代數和的取值范圍的求法,是中檔題,解題時要認真審題,注意平面向量的性質的合理運用.


 浙大優學小學年級銜接捷徑浙江大學出版社系列答案
浙大優學小學年級銜接捷徑浙江大學出版社系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
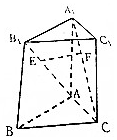 如圖,在三棱柱ABC-A1B1C1中,已知E,F分別是線段AB1與CA1上的動點,異面直線AB1與CA1所成角為θ,記線段EF中點M的軌邊為L,則|L|等于( )
如圖,在三棱柱ABC-A1B1C1中,已知E,F分別是線段AB1與CA1上的動點,異面直線AB1與CA1所成角為θ,記線段EF中點M的軌邊為L,則|L|等于( )| A. | $\frac{1}{2}$|AB1| | |
| B. | $\sqrt{{\overrightarrow{A{B}_{1}}}^{2}+{\overrightarrow{C{A}_{1}}}^{2}-(\overrightarrow{A{B}_{1}}•\overrightarrow{C{A}_{1}})^{2}}$ | |
| C. | $\frac{1}{4}$|AB1|•|CA1|•sinθ | |
| D. | $\frac{1}{12}$•V${\;}_{{\;}_{ABC-{A}_{1}{B}_{1}{C}_{1}}}$(V${\;}_{ABC-{A}_{1}{B}_{1}{C}_{1}}$是三棱柱ABC-A1B1C1的體積) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{x^2}{2}+\frac{y^2}{{\sqrt{2}}}=1$ | B. | $\frac{x^2}{2}+{y^2}=1$ | C. | $\frac{x^2}{4}+\frac{y^2}{2}=1$ | D. | $\frac{y^2}{4}+\frac{x^2}{2}=1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{6}$ | B. | 3 | C. | 6 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -12 | B. | -1 | C. | 0 | D. | $\frac{3}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com