
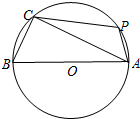
 在△ABC中,三個內角A,B,C的對邊分別為a,b,c,已知$\frac{cosA}{cosB}$=$\frac{b}{a}$=$\sqrt{3}$.
在△ABC中,三個內角A,B,C的對邊分別為a,b,c,已知$\frac{cosA}{cosB}$=$\frac{b}{a}$=$\sqrt{3}$.分析 (1)由已知結合正弦定理可得sin2A=sin2B,再由角的范圍可得A+B=$\frac{π}{2}$,從而求得C;
(2)把三角形ABC的三邊用R表示,再由S(θ)=S△ABC+S△APC,代入三角形面積公式化簡,然后由θ∈($\frac{π}{6},\frac{π}{2}$)求得四邊形APCB面積S(θ)的最大值.
解答 解:(1)由$\frac{cosA}{cosB}$=$\frac{b}{a}$,得$\frac{cosA}{cosB}$=$\frac{sinB}{sinA}$,∴sin2A=sin2B,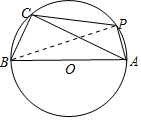
∵2A,2B∈(0,2π),∴2A=2B,或2A+2B=π,
即A=B或A+B=$\frac{π}{2}$,
∵$\frac{b}{a}=\sqrt{3}$,∴A=B舍去,從而C=$\frac{π}{2}$;
(2)由條件得:c=2R,a=R,b=$\sqrt{3}$R,∠BAC=$\frac{π}{6}$,∠CAP=θ-$\frac{π}{6}$,θ∈($\frac{π}{6},\frac{π}{2}$),
S(θ)=S△ABC+S△APC=$\frac{\sqrt{3}}{2}{R}^{2}+\frac{1}{2}AC•AP•sin(θ-\frac{π}{6})$
=$\frac{\sqrt{3}}{2}{R}^{2}+\frac{1}{2}\sqrt{3}R•2Rcosθsin(θ-\frac{π}{6})$=$\frac{\sqrt{3}}{2}{R}^{2}+\sqrt{3}{R}^{2}cosθ(\frac{\sqrt{3}}{2}sinθ-\frac{1}{2}cosθ)$
=$\frac{\sqrt{3}}{2}{R}^{2}+\frac{\sqrt{3}}{4}{R}^{2}(\sqrt{3}sin2θ-cos2θ-1)$=$\frac{\sqrt{3}}{4}{R}^{2}+\frac{\sqrt{3}}{2}{R}^{2}sin(2θ-\frac{π}{6})$,θ∈($\frac{π}{6},\frac{π}{2}$),
∵$2θ-\frac{π}{6}$∈($\frac{π}{6},\frac{5π}{6}$),
∴當$θ=\frac{π}{3}$時,$S(θ)_{max}=\frac{3\sqrt{3}}{4}{R}^{2}$.
點評 本題考查在實際問題中建立三角函數模型,考查了三角函數中的恒等變換應用,考查三角函數最值的求法,是中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 0 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 某校高一年級共有320人,為調查高一年級學生每天晚自習自主支配學習時間(指除了完成老師布置的作業后學生根據自己的需要進行學習的時間)情況,學校采用隨機抽樣的方法從高一學生中抽取了n名學生進行問卷調查.根據問卷得到了這n名學生每天晚自習自主支配學習時間的數據(單位:分鐘),按照以下區間分為七組:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到頻率分布直方圖如圖.已知抽取的學生中每天晚自習自主支配學習時間低于20分鐘的人數是4人.
某校高一年級共有320人,為調查高一年級學生每天晚自習自主支配學習時間(指除了完成老師布置的作業后學生根據自己的需要進行學習的時間)情況,學校采用隨機抽樣的方法從高一學生中抽取了n名學生進行問卷調查.根據問卷得到了這n名學生每天晚自習自主支配學習時間的數據(單位:分鐘),按照以下區間分為七組:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到頻率分布直方圖如圖.已知抽取的學生中每天晚自習自主支配學習時間低于20分鐘的人數是4人.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | -1 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com