Question

6．已知等腰梯形ABCD中，AB∥DC，∠A=∠B=60°，等腰梯形ABCD外接圓的半徑為1，則這個梯形面積S的取值范圍（0，$\frac{3}{2}$]．

Answer 1

分析 由題意：等腰梯形ABCD外接圓的半徑為1，∠A=∠B=60°，利用正弦定理可知，等腰梯形ABCD在圓內的對角線為定值$\sqrt{3}$，設對角線與底邊的夾角為θ（0＜θ＜60°），建立關系，化簡，利用三角函數的有界限即可求梯形面積S的取值范圍．

解答 解：如圖：等腰梯形ABCD外接圓的半徑為1，∠B=60°，
利用正弦定理可知，$\frac{AC}{sin60°}=2R$，
等腰梯形ABCD對角線AC=$\sqrt{3}$．
設AC與底邊的夾角為α（0＜α＜60°），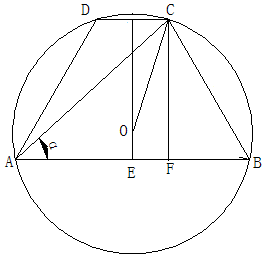
過C點作CF垂直AB，交于AB于F，
則AF=$\sqrt{3}$cosα，CF=$\sqrt{3}$sinα，
BF=sinα，DC=$\sqrt{3}$cosα-sinα，
梯形面積S=$\frac{1}{2}$（AB+DC）×CF
=$\frac{1}{2}$（$\sqrt{3}$cosα+sinα+$\sqrt{3}$cosα-sinα）×$\sqrt{3}$sinα，
=3cosαsinα，
=$\frac{3}{2}$sin2α，
∵0＜α＜60°，
∴0＜2α＜120°，
當2α=90°時，梯形面積最大值為$\frac{3}{2}$．
所以這個梯形面積S的取值范圍是（0，$\frac{3}{2}$]．
故答案為（0，$\frac{3}{2}$]

點評 本題考查了等腰梯形ABCD外接圓的問題，其圓心為腰的垂直平分線和底邊的垂直平分線的交點．利用了正弦定理可知等腰梯形ABCD在圓內的對角線為定值$\sqrt{3}$是解題的關鍵．屬于中檔題．