
分析 (1)求出函數的導數,問題轉化為x2+x+a=0存在大于0的實數根,根據y=x2+x+a在x>0時遞增,求出a的范圍即可;
(2)求出函數f(x)的導數,通過討論a的范圍,判斷導函數的符號,求出函數的單調區間即可;
(3)求出函數g(x)的導數,根據f(e)=-$\frac{a}{e}$>0,得到存在x0∈(1,e)滿足g′(x0)=0,從而得到函數的單調區間,求出函數的極小值,證出結論即可.
解答 解:(1)由f(x)=lnx-$\frac{a}{x}$-1得:
f′(x)=$\frac{x+a}{{x}^{2}}$,(x>0),
由已知曲線y=f(x)存在斜率為-1的切線,
∴f′(x)=-1存在大于0的實數根,
即x2+x+a=0存在大于0的實數根,
∵y=x2+x+a在x>0時遞增,
∴a的范圍是(-∞,0);
(2)由f′(x)=$\frac{x+a}{{x}^{2}}$,(x>0),
得:a≥0時,f′(x)>0,
∴f(x)在(0,+∞)遞增;
a<0時,若x∈(-a,+∞)時,f′(x)>0,
若x∈(0,-a),則f′(x)<0,
故f(x)在(-a,+∞)遞增,在(0,-a)遞減;
(3)由g(x)=$\frac{x+a}{lnx}$及題設得:
g′(x)=$\frac{lnx-\frac{a}{x}-1}{{(lnx)}^{2}}$=$\frac{f(x)}{{(lnx)}^{2}}$,
由-1<a<0,得:0<-a<1,
由(2)得:f(x)在(-a,+∞)遞增,
∴f(1)=-a-1<0,取x=e,顯然e>1,
f(e)=-$\frac{a}{e}$>0,
∴存在x0∈(1,e)滿足f(x0)=0,
即存在x0∈(1,e)滿足g′(x0)=0,
令g′(x)>0,解得:x>x0,
令g′(x)<0,解得:1<x<x0,
故g(x)在(1,x0)遞減,在(x0,+∞)遞增,
∴-1<a<0時,g(x)在(1,+∞)存在極小值.
點評 本題考查了函數的單調性、最值問題,考查導數的應用以及分類討論思想、是一道綜合題.


 學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目:高中數學 來源: 題型:選擇題
| A. | ($\frac{1}{3}$,$\frac{2}{3}$) | B. | [$\frac{1}{3}$,$\frac{2}{3}$) | C. | ($\frac{1}{2}$,$\frac{2}{3}$) | D. | [$\frac{1}{2}$,$\frac{2}{3}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
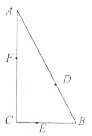 如圖,某公園有三條觀光大道AB,BC,AC圍成直角三角形,其中直角邊BC=200m,斜邊AB=400m,現有甲、乙、丙三位小朋友分別在AB,BC,AC大道上嬉戲,所在位置分別記為點D,E,F.
如圖,某公園有三條觀光大道AB,BC,AC圍成直角三角形,其中直角邊BC=200m,斜邊AB=400m,現有甲、乙、丙三位小朋友分別在AB,BC,AC大道上嬉戲,所在位置分別記為點D,E,F.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
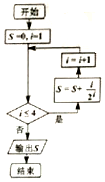
| A. | $\frac{15}{16}$ | B. | $\frac{15}{12}$ | C. | $\frac{13}{8}$ | D. | $\frac{13}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 如果a1是5的倍數,那么數列{an}與數列{2n}必有相同的項 | |
| B. | 如果a1不是5的倍數,那么數列{an}與數列{2n}必沒有相同的項 | |
| C. | 如果a1不是5的倍數,那么數列{an}與數列{2n}只有有限個相同的項 | |
| D. | 如果a1不是5的倍數,那么數列{an}與數列{2n}有無窮多個相同的項. |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -3 | B. | 3 | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com