
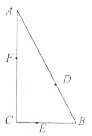
 如圖,某公園有三條觀光大道AB,BC,AC圍成直角三角形,其中直角邊BC=200m,斜邊AB=400m,現有甲、乙、丙三位小朋友分別在AB,BC,AC大道上嬉戲,所在位置分別記為點D,E,F.
如圖,某公園有三條觀光大道AB,BC,AC圍成直角三角形,其中直角邊BC=200m,斜邊AB=400m,現有甲、乙、丙三位小朋友分別在AB,BC,AC大道上嬉戲,所在位置分別記為點D,E,F.分析 (1)由題意,BD=300,BE=100,△BDE中,由余弦定理可得甲乙兩人之間的距離;
(2)△BDE中,由正弦定理可得$\frac{200-2ysinθ}{sinθ}$=$\frac{y}{sin60°}$,可將甲乙之間的距離y表示為θ的函數,并求甲乙之間的最小距離.
解答 解:(1)由題意,BD=300,BE=100,
△ABC中,cosB=$\frac{1}{2}$,B=$\frac{π}{3}$,
△BDE中,由余弦定理可得DE=$\sqrt{30{0}^{2}+10{0}^{2}-2•300•100•\frac{1}{2}}$=100$\sqrt{7}$m;
(2)由題意,EF=2DE=2y,∠BDE=∠CEF=θ.
△CEF中,CE=EFcos∠CEF=2ycosθ
△BDE中,由正弦定理可得$\frac{200-2ycosθ}{sinθ}$=$\frac{y}{sin60°}$,
∴y=$\frac{100\sqrt{3}}{sinθ+\sqrt{3}cosθ}$=$\frac{50\sqrt{3}}{sin(θ+\frac{π}{3})}$,0$<θ<\frac{π}{2}$,
∴θ=$\frac{π}{6}$,ymin=50$\sqrt{3}$m.
點評 本題考查利用數學知識解決實際問題,考查正弦、余弦定理的運用,考查學生分析解決問題的能力,屬于中檔題.


 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優練測系列答案
世紀百通優練測系列答案 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
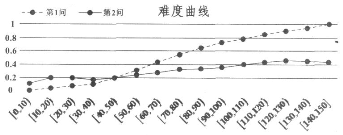
| A. | 此題沒有考生得12分 | |
| B. | 此題第1問比第2問更能區分學生數學成績的好與壞 | |
| C. | 分數在[40,50)的考生此大題的平均得分大約為4.8分 | |
| D. | 全體考生第1問的得分標準差小于第2問的得分標準差 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com