
| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
分析 作出不等式組對應的平面區域,利用幾何概型的概率公式,求出相應的面積即可得到結論.
解答 解:作出不等式組對應的平面區域,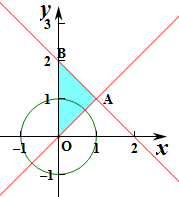 對應區域為△OAB,
對應區域為△OAB,
則三角形的面積為S=$\frac{1}{2}$×1×2=1,
點P取自圓x2+y2=2內部的面積為圓面積的$\frac{1}{4}$,即$\frac{1}{4}$×π×${(\sqrt{2})}^{2}$=$\frac{π}{2}$,
則根據幾何概型的概率公式可得,
則點P取自圓x2+y2=2內部的概率等于$\frac{π}{2}$.
故選:C.
點評 本題主要考查幾何概型的概率的計算,根據條件求出相應的面積是解決本題的關鍵.利用數形結合是解決此類問題的基本方法.


 教學練新同步練習系列答案
教學練新同步練習系列答案 課前課后同步練習系列答案
課前課后同步練習系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 日期 | 2月11日 | 2月12日 | 2月13日 | 2月14日 | 2月15日 | 2月16日 |
| 平均氣溫x(℃) | 10 | 11 | 13 | 12 | 8 | 6 |
| 飲料銷量y(杯) | 22 | 25 | 29 | 26 | 16 | 12 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充分必要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
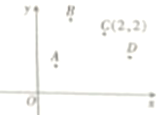 如圖,A,B,C,D是平面直角坐標系上的四個點,將這四個點的坐標(x,y)分別代入x-y=k,若在某點處k取得最大值,則該點是( )
如圖,A,B,C,D是平面直角坐標系上的四個點,將這四個點的坐標(x,y)分別代入x-y=k,若在某點處k取得最大值,則該點是( )| A. | 點A | B. | 點B | C. | 點C | D. | 點D |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com