欧美综合一区,精品一区二区三区免费毛片爱,91玖玖

17．函數f（x）=x-sinx（x∈R），則f（x）（　　）

	A．	是奇函數，且在（-∞，+∞）上是減函數		B．	是偶函數，且在（-∞，+∞）上是減函數
	C．	是偶函數，且在（-∞，+∞）上是增函數		D．	是奇函數，且在（-∞，+∞）上是增函數

分析利用奇函數的定義，驗證f（-x）=-x+sinx=-f（x），利用導數非負，確定函數f（x）=x-sinx（x∈R）在（-∞，+∞）上是增函數．

解答解：∵f（-x）=-x-sin（-x）=-x+sinx=-（x-sinx）=-f（x），
∴函數f（x）是奇函數．
求導函數可得f′（x）=1-cosx．
∵-1≤cosx≤1，
∴f′（x）=1-cosx≥0．
∴函數f（x）=x-sinx（x∈R）在（-∞，+∞）上是增函數．
故選：D．

點評本題考查了函數奇偶性的判定，考查了利用導數研究函數的單調性，是基礎題．

練習冊系列答案

復習計劃風向標暑系列答案

開心快樂假期作業暑假作業西安出版社系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：選擇題

12．過原點且與圓x²+y²-4x+3=0相切的直線的傾斜角為（　　）

A．

$\frac{π}{3}$或$\frac{2π}{3}$

B．

$\frac{π}{6}$或$\frac{5π}{6}$

C．

$\frac{π}{4}$或$\frac{3π}{4}$

D．

$\frac{π}{3}$或$\frac{5π}{6}$

查看答案和解析>>

科目：高中數學 來源： 題型：填空題

13．已知圓C：（x-m）²+（y-n）²=9的圓心在第一象限，直線l：x+2y+2=0與圓C相交的弦長為4，則$\frac{m+2n}{mn}$的最小值為$\frac{8}{3}$．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

5．在△ABC中，內角A，B，C所對的邊分別是a，b，c，已知$csinA=\sqrt{3}acosC$，（a-c）（a+c）=b（b-c），函數$f（x）=2sinxcos（\frac{π}{2}-x）-\sqrt{3}sin（π+x）cosx+sin（\frac{π}{2}+x）cosx$
（1）求函數y=f（x）的周期和對稱軸方程；
（2）求f（B）的值．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

12．

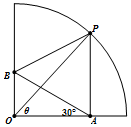現有四分之一圓形的紙板（如圖），∠AOB=90°，圓半徑為1，要裁剪成四邊形OAPB，且滿足AP∥OB，∠OAB=30°，∠POA=θ，記此四邊形OAPB的面積為f（θ），求f（θ）的最大值．

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

2．

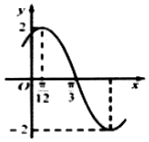已知函數f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分圖象如圖所示，若將f（x）圖象上所有點向右平移$\frac{π}{12}$個單位得到函數g（x）的圖象，則函數g（x）的單調遞減區間為（　　）

	A．	[kπ-$\frac{π}{3}$，kπ+$\frac{π}{6}$]，k∈Z		B．	[kπ+$\frac{π}{6}$，kπ+$\frac{2π}{3}$]，k∈Z
	C．	[kπ-$\frac{π}{12}$，kπ+$\frac{π}{12}$]，k∈Z		D．	[kπ-$\frac{7π}{12}$，kπ-$\frac{π}{12}$]，k∈Z

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

9．已知集合A={x|2^x＞1}，B={x|x²-3x-4＞0}，則∁_R（A∪B）=（　　）

A．

{x|x≤0或x＞4}

B．

{x|x＜-1或x＞4}

C．

D．

{x|-1≤x≤0}

查看答案和解析>>

科目：高中數學 來源： 題型：填空題

6．我們知道，如果定義在某區間上的函數f（x）滿足對該區間上的任意兩個數x₁，x₂，總有不等式$\frac{{f（{x_1}）+f（{x_2}）}}{2}≤f（{\frac{{{x_1}+{x_2}}}{2}}）$成立，則稱函數f（x）在該區間上的向上凸函數（簡稱上凸）．類比上述定義，對于數列{a_n}，如果對任意正整數n，總有不等式$\frac{{{a_n}+{a_{n+2}}}}{2}≤{a_{n+1}}$成立，則稱數列{a_n}為向上凸數列（簡稱上凸數列），現有數列{a_n}滿足如下兩個條件：
①數列{a_n}為上凸數列，且a₁=1，a₁₀=28；
②對正整數n（1≤n＜10，n∈N^*），都有|a_n-b_n|≤20，其中${b_n}={n^2}-6n+10$，則數列{a_n}中的第三項a₃的取值范圍為[7，19]．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

7．f（x）=x²-2x+alnx．
（Ⅰ）若a=2，求f（x）在點（1，f（1））處的切線方程；
（Ⅱ）討論f（x）的單調性．

查看答案和解析>>

同步練習冊答案

日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

練習冊

高中

初中

小學