
| A. | $(-∞,-\frac{5}{2}]$ | B. | $(-\frac{5}{2},-\frac{3}{2}]$ | C. | $[-\frac{5}{2},-\frac{3}{2}]$ | D. | $(-\frac{3}{2},+∞)$ |
分析 方程$f(x)-ax=\frac{5}{2}$有3個不同的解,即$f(x)=ax+\frac{5}{2}$有3個不同的解,等價于y=f(x)與$y=ax+\frac{5}{2}$的圖象有3個不同的交點,因為直線$y=ax+\frac{5}{2}$恒過$({0,\;\;\frac{5}{2}})$,所以滿足條件的直線應在圖中的l1與l2之間,求出斜率,即可得出結論.
解答  解:f(x)的圖象如圖所示,方程$f(x)-ax=\frac{5}{2}$有3個不同的解,即$f(x)=ax+\frac{5}{2}$有3個不同的解,
解:f(x)的圖象如圖所示,方程$f(x)-ax=\frac{5}{2}$有3個不同的解,即$f(x)=ax+\frac{5}{2}$有3個不同的解,
等價于y=f(x)與$y=ax+\frac{5}{2}$的圖象有3個不同的交點,
因為直線$y=ax+\frac{5}{2}$恒過$({0,\;\;\frac{5}{2}})$,
所以滿足條件的直線應在圖中的l1與l2之間,斜率分別是${k_1}=\frac{{\frac{5}{2}-1}}{0-1}=-\frac{3}{2}$,${k_2}=\frac{{\frac{5}{2}-0}}{0-1}=-\frac{5}{2}$,故$a∈({-\frac{5}{2},\;\;-\frac{3}{2}}]$,
故選B.
點評 本題考查方程解的研究,考查數形結合的數學思想,考查學生分析解決問題的能力,正確轉化是關鍵.


科目:高中數學 來源: 題型:解答題
 如圖,四邊形ABCD是平行四邊形,平面AED⊥平面ABCD,EF∥AB,$BC=EF=\frac{1}{2}AB$,∠BAD=60°,G為BC的中點.
如圖,四邊形ABCD是平行四邊形,平面AED⊥平面ABCD,EF∥AB,$BC=EF=\frac{1}{2}AB$,∠BAD=60°,G為BC的中點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
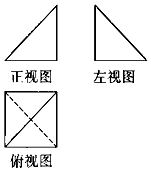 如圖1,一個多面體的正視圖和側視圖是兩個全等的等腰直角三角形且直角邊長為2,俯視圖是邊長為2的正方形,則該多面體的表面積是( )
如圖1,一個多面體的正視圖和側視圖是兩個全等的等腰直角三角形且直角邊長為2,俯視圖是邊長為2的正方形,則該多面體的表面積是( )| A. | $2+4\sqrt{2}+2\sqrt{3}$ | B. | $2+4\sqrt{2}+\sqrt{6}$ | C. | $2+4\sqrt{2}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 某中學高三年級有400名學生參加月考,用簡單隨機抽樣的方法抽取了一個容量為50的樣本,得到數學成績的頻率分布直方圖如圖所示.
某中學高三年級有400名學生參加月考,用簡單隨機抽樣的方法抽取了一個容量為50的樣本,得到數學成績的頻率分布直方圖如圖所示.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 奇函數,且在區間$(0,\frac{π}{2})$上單調遞增 | B. | 奇函數,且在區間$(0,\frac{π}{2})$上單調遞減 | ||
| C. | 偶函數,且在區間$(0,\frac{π}{2})$上單調遞增 | D. | 偶函數,且在區間$(0,\frac{π}{2})$上單調遞減 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com