
 如圖,四邊形ABCD是平行四邊形,平面AED⊥平面ABCD,EF∥AB,$BC=EF=\frac{1}{2}AB$,∠BAD=60°,G為BC的中點.
如圖,四邊形ABCD是平行四邊形,平面AED⊥平面ABCD,EF∥AB,$BC=EF=\frac{1}{2}AB$,∠BAD=60°,G為BC的中點.分析 (1)令BD中點為O,連結GO,EO,只需證明FG∥EO即可,
(2)只需證明BD⊥面EAD即可.
解答 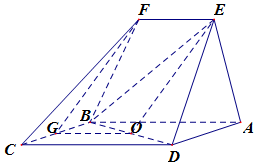 解:(1)令BD中點為O,∵GO∥AB,且$GO=\frac{1}{2}AB$,EF∥AB,且$EF=\frac{1}{2}AB$,
解:(1)令BD中點為O,∵GO∥AB,且$GO=\frac{1}{2}AB$,EF∥AB,且$EF=\frac{1}{2}AB$,
∴GO∥EF,且GO=EF,四邊形GOEF是平行四邊形,得FG∥EO,
又∵FG?面BED,EO?面BED,∴FG∥面BED.
(2)∵$∠BAO={60°},BC=\frac{1}{2}AB$,
∴∠BDA=90°,即BD⊥AD;
又∵面AED⊥面ABCD,且交線為AD,
∴BD⊥面EAD,面BED⊥面EAD.
點評 本題考查了線面平行,面面垂直的判定,屬于基礎題.


科目:高中數學 來源: 題型:選擇題
| A. | -1 | B. | 0 | C. | 1 | D. | 2016 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 直線a必垂直于平面β | B. | 直線b必垂直于平面α | ||
| C. | 直線a不一定垂直于平面β | D. | 過a的平面與過b的平面垂直 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
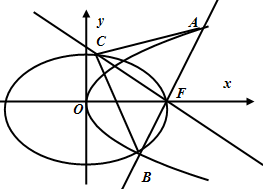 如圖,設橢圓C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),長軸的右端點與拋物線C2:y2=8x的焦點F重合,且橢圓C1的離心率是$\frac{\sqrt{3}}{2}$.
如圖,設橢圓C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),長軸的右端點與拋物線C2:y2=8x的焦點F重合,且橢圓C1的離心率是$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\left.{\begin{array}{l}{m⊥n}\\{n?α}\end{array}}\right\}⇒m⊥α$ | B. | $\left.{\begin{array}{l}{m⊥n}\\{n⊥α}\end{array}}\right\}⇒m∥α$ | C. | $\left.{\begin{array}{l}{m⊥α}\\{n∥α}\end{array}}\right\}⇒m⊥n$ | D. | $\left.{\begin{array}{l}{m∥α}\\{n?α}\end{array}}\right\}⇒m∥n$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
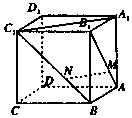 正方體ABCD-A1B1C1D1中,點M、N分別在線段AB1、BC1上,且AM=BN.以下結論:①AA1⊥MN;②A1C1∥MN;③MN∥平面A1B1C1D1;④MN與A1C1異面,⑤MN與 A1C1成30°.其中有可能成立的結論的個數為( )
正方體ABCD-A1B1C1D1中,點M、N分別在線段AB1、BC1上,且AM=BN.以下結論:①AA1⊥MN;②A1C1∥MN;③MN∥平面A1B1C1D1;④MN與A1C1異面,⑤MN與 A1C1成30°.其中有可能成立的結論的個數為( )| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 只要將函數y=2sin3x的圖象向右平移$\frac{π}{3}$個單位 | |
| B. | 只要將函數y=sin3x的圖象向右平移$\frac{π}{3}$個單位 | |
| C. | 只要將函數y=2sin3x的圖象向右平移$\frac{π}{9}$個單位 | |
| D. | 只要將函數y=sin3x的圖象向右平移$\frac{π}{9}$個單位 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(-∞,-\frac{5}{2}]$ | B. | $(-\frac{5}{2},-\frac{3}{2}]$ | C. | $[-\frac{5}{2},-\frac{3}{2}]$ | D. | $(-\frac{3}{2},+∞)$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com