
分析 若甲正確,則乙、丙均錯誤,從而可得甲為第三名,且乙、丙中必有一人正確,一人錯誤,再假設丙錯誤(則乙正確),可導出矛盾,從而可得丙為第二名,故得答案.
解答 解:若甲正確,則乙、丙均錯誤,故丙是第一名,乙是第二名,甲是第三名,與“甲說:我不是第三名“正確相矛盾,
故甲錯誤,因此,甲為第三名;①
于是乙、丙中必有一人正確,一人錯誤.
若丙錯誤(則乙正確),即丙是第一名,而甲是第三名,故乙是第二名,與乙正確”我是第三名“矛盾,故丙正確,即丙不是第一名,為第二名;②
由①②得:獲得第一名的是:乙.
故答案為:乙.
點評 本題考查合情推理,突出反證法在推理中的應用,考查推理分析能力,屬于中檔題.


 黃岡經典趣味課堂系列答案
黃岡經典趣味課堂系列答案 啟東小題作業本系列答案
啟東小題作業本系列答案科目:高中數學 來源: 題型:選擇題
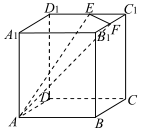 如圖所示,在棱長為 6的正方體ABCD-A1B1C1D1中,點E,F分別是棱C1D1,B1C1的中點,過A,E,F三點作該正方體的截面,則截面的周長為( )
如圖所示,在棱長為 6的正方體ABCD-A1B1C1D1中,點E,F分別是棱C1D1,B1C1的中點,過A,E,F三點作該正方體的截面,則截面的周長為( )| A. | $18+3\sqrt{2}$ | B. | $6\sqrt{13}+3\sqrt{2}$ | C. | $6\sqrt{5}+9\sqrt{2}$ | D. | $10+3\sqrt{2}+4\sqrt{10}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com