
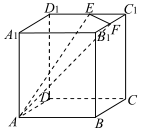
 如圖所示,在棱長為 6的正方體ABCD-A1B1C1D1中,點(diǎn)E,F(xiàn)分別是棱C1D1,B1C1的中點(diǎn),過A,E,F(xiàn)三點(diǎn)作該正方體的截面,則截面的周長為( )
如圖所示,在棱長為 6的正方體ABCD-A1B1C1D1中,點(diǎn)E,F(xiàn)分別是棱C1D1,B1C1的中點(diǎn),過A,E,F(xiàn)三點(diǎn)作該正方體的截面,則截面的周長為( )| A. | $18+3\sqrt{2}$ | B. | $6\sqrt{13}+3\sqrt{2}$ | C. | $6\sqrt{5}+9\sqrt{2}$ | D. | $10+3\sqrt{2}+4\sqrt{10}$ |
分析 由題意畫出截面五邊形,再由已知利用勾股定理求得邊長得答案.
解答 解:如圖,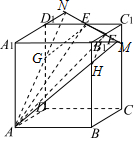
延長EF、A1B1 相交于M,連接AM交BB1 于H,
延長FE、A1D1 相交于N,連接AN交DD1 于G,
可得截面五邊形AHFEG.
∵ABCD-A1B1C1D1是邊長為6的正方體,且E,F(xiàn)分別是棱C1D1,B1C1的中點(diǎn),
∴EF=3$\sqrt{2}$,AG=AH=$\sqrt{{6}^{2}+{4}^{2}}=2\sqrt{13}$,EG=FH=$\sqrt{{3}^{2}+{2}^{2}}=\sqrt{13}$.
∴截面的周長為$6\sqrt{13}+3\sqrt{2}$.
故選:B.
點(diǎn)評 本題考查棱柱的結(jié)構(gòu)特征,考查空間想象能力和思維能力,是中檔題.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
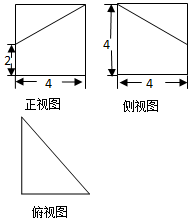
| A. | $\frac{32}{3}$ | B. | $\frac{50}{3}$ | C. | $\frac{64}{3}$ | D. | $\frac{80}{3}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com