
分析 (Ⅰ)先求出函數g(x)=x-x3+x2-2,的導函數,利用導函數求出原函數的單調區間,進而求出其極大值、極小值;
(Ⅱ)先求出其導函數,把函數f(x)在(-$\frac{1}{3}$,+∞)上恒為單調遞增函數,轉化為其導函數的最小值恒大于等于0,利用二次函數在固定區間上求最值的方法求出導函數的最小值,再與0比即可求出實數a的取值范圍.
解答 解:(Ⅰ)當a=-1,f(x)=x3-x2+x+2,g(x)=x-x3+x2-2,求導,g′(x)=-3x2+2x+1,
令g′(x)=0,解得:x=-$\frac{1}{3}$,x=1,
| x | (-∞,-$\frac{1}{3}$) | -$\frac{1}{3}$ | (-$\frac{1}{3}$,1) | 1 | (1,+∞) |
| g′(x) | - | 0 | + | 0 | - |
| g(x) | ↘ | -$\frac{59}{27}$ | ↗ | -1 | ↘ |
點評 本題考查利用導函數來研究函數的極值.在利用導函數來研究函數的極值時,分三步①求導函數,②求導函數為0的根,③判斷根左右兩側的符號,若左正右負,原函數取極大值;若左負右正,原函數取極小值,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
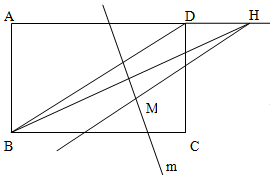 如圖所示,ABCD是長為8,寬為4的矩形,設點H在直線AD上運動,BH的垂直平分線為m,過點H且與BD平行(或重合)的直線與直線m相交于點M,則點M的軌跡為( )
如圖所示,ABCD是長為8,寬為4的矩形,設點H在直線AD上運動,BH的垂直平分線為m,過點H且與BD平行(或重合)的直線與直線m相交于點M,則點M的軌跡為( )| A. | 圓的一部分 | B. | 橢圓的一部分 | C. | 雙曲線的一部分 | D. | 拋物線的一部分 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
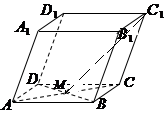 四棱柱ABCD-A1B1C1D1的底面是平行四邊形,M是AC與BD的交點.若$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,$\overrightarrow{A{A_1}}$=$\overrightarrow c$,則$\overrightarrow{{C_1}M}$可以表示為( )
四棱柱ABCD-A1B1C1D1的底面是平行四邊形,M是AC與BD的交點.若$\overrightarrow{AB}$=$\overrightarrow a$,$\overrightarrow{AD}$=$\overrightarrow b$,$\overrightarrow{A{A_1}}$=$\overrightarrow c$,則$\overrightarrow{{C_1}M}$可以表示為( )| A. | $\overrightarrow a+\overrightarrow b+\frac{1}{2}\overrightarrow c$ | B. | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ | C. | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b-\overrightarrow c$ | D. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com