
分析 (1)設切點T(x0,y0)則kAT=f′(x0),由此能求出切線方程
(2)由f(x)≥-x2+ax-6在(0,+∞)上恒成立,知a≤lnx+x+$\frac{6}{x}$,設g(x)=lnx+x+$\frac{6}{x}$,由此能夠求出實數a的取值范圍.
解答 解:設切點T(x0,y0)則kAT=f′(x0),
∴$\frac{{x}_{0}ln{x}_{0}}{{x}_{0}+\frac{1}{{e}^{2}}}$=lnx0+1即e2x0+lnx0+1=0
設h(x)=e2x+lnx+1,當x>0時h′(x)>0,
∴h(x)是單調遞增函數,
∴h(x)=0最多只有一個根,
又h($\frac{1}{{e}^{2}}$)=e2×$\frac{1}{{e}^{2}}$+ln$\frac{1}{{e}^{2}}$+1=0,
∴x0=$\frac{1}{{e}^{2}}$
由f'(x0)=-1得切線方程是x+y+$\frac{1}{{e}^{2}}$=0.
(2)∵f(x)≥-x2+ax-6在(0,+∞)上恒成立,
∴a≤lnx+x+$\frac{6}{x}$,
設g(x)=lnx+x+$\frac{6}{x}$,
則g′(x)=$\frac{{x}^{2}+x-6}{{x}^{2}}$=$\frac{(x+3)(x-2)}{{x}^{2}}$,
當x>2時,g′(x)>0,函數g(x)是增函數,
當0<x<2時,g′(x)<0,函數g(x)是減函數,
∴a≤g(2)=5+ln2.
即實數a的取值范圍是(-∞,5+ln2].
點評 本題考查利用導數求函數的單調區間和實數的取值范圍的方法,解題時要認真審題,仔細解答,注意分類討論思想和等價轉化思想的合理運用.


 名題訓練系列答案
名題訓練系列答案 期末集結號系列答案
期末集結號系列答案科目:高中數學 來源: 題型:解答題
 如圖,四棱錐P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=$2\sqrt{2}$.
如圖,四棱錐P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=$2\sqrt{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | t>10 | B. | t<10 | C. | t>30 | D. | t<30 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
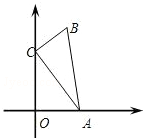 如圖,在△ABC中,∠ACB=90°,AC=2,BC=1,點A、C分別在x軸、y軸上,當點A在x軸上運動時,點C隨之在y軸上運動,在運動過程中,點B到原點O的最大距離是1+$\sqrt{2}$.
如圖,在△ABC中,∠ACB=90°,AC=2,BC=1,點A、C分別在x軸、y軸上,當點A在x軸上運動時,點C隨之在y軸上運動,在運動過程中,點B到原點O的最大距離是1+$\sqrt{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com