Question

19．已知P為△ABC內一點，且5$\overrightarrow{AP}$-2$\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{0}$，則△PAC的面積與△ABC的面積之比等于$\frac{2}{5}$．

Answer 1

分析 由5$\overrightarrow{AP}$-2$\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{0}$，可得$\overrightarrow{AP}$=$\frac{2}{5}\overrightarrow{AB}$+$\frac{1}{5}$$\overrightarrow{AC}$，延長AP交BC于D，則$\frac{5}{3}\overrightarrow{AP}$=$\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}$$\overrightarrow{AC}$=$\overrightarrow{AD}$，從而可以得到D是BC邊的三等分點，且CD=$\frac{2}{3}$CB，即可得出．

解答 解：∵5$\overrightarrow{AP}$-2$\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{0}$，∴$\overrightarrow{AP}$=$\frac{2}{5}\overrightarrow{AB}$+$\frac{1}{5}$$\overrightarrow{AC}$，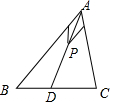
延長AP交BC于D，則$\frac{5}{3}\overrightarrow{AP}$=$\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}$$\overrightarrow{AC}$=$\overrightarrow{AD}$，
從而可以得到D是BC邊的三等分點，且CD=$\frac{2}{3}$CB，
設點B到邊AC的距離為d，則點P到邊AC的距離為$\frac{2}{3}$×$\frac{3}{5}$d=$\frac{2}{5}$d，
所以△PAC的面積與△ABC的面積之比為$\frac{2}{5}$．
故答案為：$\frac{2}{5}$．

點評 本題考查了向量線性運算法則、向量共線定理、三角形面積計算公式，考查了推理能力與計算能力，屬于中檔題．