
| A. | {x|x>2} | B. | {x|0<x<2} | C. | {x|x>$\frac{1}{2}$} | D. | {x|0<x<$\frac{1}{2}$} |
分析 根據兩個不等式的關系,只要令$\frac{1}{t}$=x,則關于t的不等式ln$\frac{1}{t}$>$\frac{a}{t}$-1,得到$\frac{1}{t}$的范圍,即求得x的范圍.
解答 解:令$\frac{1}{t}$=x,則關于t的不等式ln$\frac{1}{t}$>$\frac{a}{t}$-1
即lnt<1-$\frac{a}{t}$的解集為{$\frac{1}{t}$|$\frac{1}{t}$>2},
所以所以{t|0<t<$\frac{1}{2}$},
所以不等式lnx<1-$\frac{a}{x}$的解集為{x|0<x<$\frac{1}{2}$};
故選D.
點評 本題考查了抽象不等式的解法;本題的關鍵是發現兩個不等式的未知數關系是倒數關系.


 一本好題口算題卡系列答案
一本好題口算題卡系列答案科目:高中數學 來源: 題型:選擇題
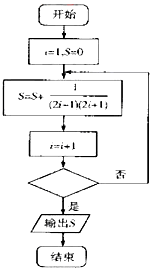
| A. | i>2014 | B. | i>2014 | C. | i>2015 | D. | i>2017 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
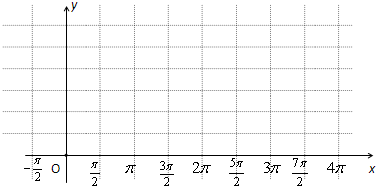
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com