
分析 (1)利用余弦函數的圖象的圖象的對稱性,求得f(x)的對稱軸和對稱中心.
(2)利用余弦函數的定義域和值域,求得函數的最值,以及取得最值時的x值.
解答 解:(1)對于f(x)=$\sqrt{2}$cos(2x-$\frac{π}{4}$),令2x-$\frac{π}{4}$=kπ,求得x=$\frac{kπ}{2}$+$\frac{π}{8}$,
可得函數的對稱軸為x=$\frac{kπ}{2}$+$\frac{π}{8}$,k∈Z.
令2x-$\frac{π}{4}$=kπ+$\frac{π}{2}$,求得x=$\frac{kπ}{2}$+$\frac{5π}{8}$,可得函數的對稱中心為($\frac{kπ}{2}$+$\frac{5π}{8}$,0),k∈Z.
(2)因為在[-$\frac{π}{8}$,$\frac{π}{2}$]上,2x-$\frac{π}{4}$∈(-$\frac{π}{2}$,$\frac{3π}{4}$),
故當2x-$\frac{π}{4}$=0時,函數f(x)取得最大值為$\sqrt{2}$,此時,x=$\frac{π}{8}$;
當2x-$\frac{π}{4}$=$\frac{3π}{4}$時,函數f(x)取得最小值為$\sqrt{2}$•(-$\frac{\sqrt{2}}{2}$)=-1,此時,x=$\frac{π}{2}$.
點評 本題主要考查余弦函數的圖象的圖象的對稱性,余弦函數的定義域和值域,屬于中檔題.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:高中數學 來源: 題型:解答題
| 日 期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
| 溫差x(°C) | 10 | 11 | 13 | 12 | 8 |
| 發芽數y(顆) | 23 | 25 | 30 | 26 | 16 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
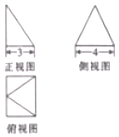 某幾何體的三視圖如圖所示,其側視圖是一個等邊三角形,則此幾何體的體積是( )
某幾何體的三視圖如圖所示,其側視圖是一個等邊三角形,則此幾何體的體積是( )| A. | 24$\sqrt{3}$ | B. | 8$\sqrt{3}$ | C. | 16$\sqrt{3}$ | D. | 16 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com