Question

8．已知F₁，F₂為雙曲線E：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右兩個焦點，點M在E上，MF₁與x軸垂直，sin∠MF₂F₁=$\frac{1}{3}$，則E的離心率為$\sqrt{2}$．

Answer 1

分析 根據雙曲線的定義，結合直角三角形的勾股定理建立方程關系進行求解即可．

解答 解：∵MF₁與x軸垂直，sin∠MF₂F₁=$\frac{1}{3}$，
∴設MF₁=m，則MF₂=3m，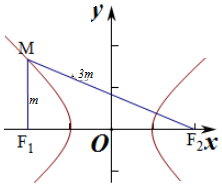
由雙曲線的定義得3m-m=2a，即2m=2a，得m=a，
在直角三角形MF₂F₁中，9m²-m²=4c²，即8m²=4c²，
即8a²=4c²，
即2a²=c²，
則$\sqrt{2}$a=c，
則e=$\frac{c}{a}$=$\sqrt{2}$，
故答案為：$\sqrt{2}$．

點評 本題主要考查雙曲線離心率的計算，根據雙曲線的定義結合直角三角形的勾股定理，結合雙曲線離心率的定4義是解決本題的關鍵．