
分析 以A為原點,以AC所在的直線為x軸,建立如圖所示的直角坐標系,設△ABC中的邊BC,AC,AB,分別為a,b,c,可得D($\frac{1}{2}$ccosA,$\frac{1}{2}$csinA),E($\frac{2}{3}$b,0),$\overrightarrow{BE}$=($\frac{2}{3}$b-ccosA,-csinA),$\overrightarrow{CD}$=($\frac{1}{2}$ccosA-b,$\frac{1}{2}$csinA),由$\overrightarrow{BE}$•$\overrightarrow{CD}$=($\frac{2}{3}$b-ccosA)•($\frac{1}{2}$ccosA-b)-$\frac{1}{2}$c2sin2A=0,得$\frac{4}{3}$bccosA-$\frac{2}{3}{b}^{2}$-$\frac{1}{2}$c2(cos2A+sin2A)=0,cosA=$\frac{\frac{1}{2}{c}^{2}+\frac{2}{3}{b}^{2}}{\frac{4}{3}bc}$$≥\frac{2\sqrt{\frac{1}{3}}}{\frac{4}{3}bc}bc$=$\frac{\sqrt{3}}{2}$,即可求解
解答 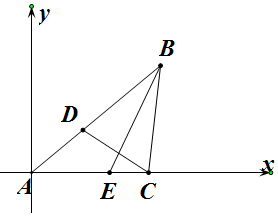 解:以A為原點,以AC所在的直線為x軸,建立如圖所示的直角坐標系,
解:以A為原點,以AC所在的直線為x軸,建立如圖所示的直角坐標系,
設△ABC中的邊BC,AC,AB,分別為a,b,c,
∴A(0,0),C(b,0),B(ccosA,csinA),
∵$AD=\frac{1}{2}AB$,$AE=\frac{2}{3}AC$,
∴D($\frac{1}{2}$ccosA,$\frac{1}{2}$csinA),E($\frac{2}{3}$b,0),
∴$\overrightarrow{BE}$=($\frac{2}{3}$b-ccosA,-csinA),$\overrightarrow{CD}$=($\frac{1}{2}$ccosA-b,$\frac{1}{2}$csinA),
∵BE⊥CD,
∴$\overrightarrow{BE}$•$\overrightarrow{CD}$=($\frac{2}{3}$b-ccosA)•($\frac{1}{2}$ccosA-b)-$\frac{1}{2}$c2sin2A=0,
∴$\frac{4}{3}$bccosA-$\frac{2}{3}{b}^{2}$-$\frac{1}{2}$c2(cos2A+sin2A)=0,
∴cosA=$\frac{\frac{1}{2}{c}^{2}+\frac{2}{3}{b}^{2}}{\frac{4}{3}bc}$$≥\frac{2\sqrt{\frac{1}{3}}}{\frac{4}{3}bc}bc$=$\frac{\sqrt{3}}{2}$,
∴$sinA≤\sqrt{1-\frac{3}{4}}=\frac{1}{2}$,
則sinA的最大值為$\frac{1}{2}$,
故答案為:$\frac{1}{2}$.
點評 本題考查了向量與三角的綜合應用,考查了建立坐標系處理平面幾何問題的解題策略,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
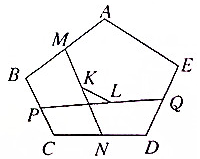 如圖所示,五邊形ABC 中,點M、N、P、Q分別是AB、CD、BC、DE的中點,K和L分別是MN和PQ的中點.求證:$\overrightarrow{KL}$=$\frac{1}{4}$$\overrightarrow{AE}$.
如圖所示,五邊形ABC 中,點M、N、P、Q分別是AB、CD、BC、DE的中點,K和L分別是MN和PQ的中點.求證:$\overrightarrow{KL}$=$\frac{1}{4}$$\overrightarrow{AE}$.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a≥-2 | B. | a<-2 | C. | a≤-2 | D. | a>-2 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com