
分析 運用兩角和的余弦公式和誘導公式、二次函數的配方化簡函數f(x),再由正弦函數的最值和二次函數的最值求法,即可得到所求最大值.
解答 解:f(x)=$\frac{2-cos[\frac{π}{4}(1-x)]+sin[\frac{π}{4}(1-x)]}{{x}^{2}+4x+5}$
=$\frac{2-\sqrt{2}cos(\frac{π}{4}-\frac{π}{4}x+\frac{π}{4})}{(x+2)^{2}+1}$
=$\frac{2-\sqrt{2}cos(\frac{π}{2}-\frac{π}{4}x)}{(x+2)^{2}+1}$=$\frac{2-\sqrt{2}sin(\frac{π}{4}x)}{(x+2)^{2}+1}$,
由-4≤x≤0,可得x=-2時,(x+2)2+1取得最小值1,
2-$\sqrt{2}$sin($\frac{π}{4}$x)在x=-2處取得最大值2+$\sqrt{2}$.
則f(x)的最大值為2+$\sqrt{2}$.
故答案為:2+$\sqrt{2}$.
點評 本題考查函數的最值的求法,注意運用兩角和的余弦公式以及誘導公式、正弦函數的值域,以及二次函數的最值求法,考查運算能力,屬于中檔題.


 優翼小幫手同步口算系列答案
優翼小幫手同步口算系列答案科目:高中數學 來源: 題型:選擇題
| A. | 12 | B. | 18 | C. | 21 | D. | 24 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1365石 | B. | 336石 | C. | 168石 | D. | 134石 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
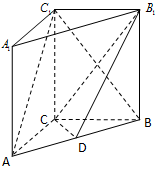 如圖,在三棱柱ABC-A1B1C1中側棱垂直于底面,AC⊥BC,點D是AB的中點.
如圖,在三棱柱ABC-A1B1C1中側棱垂直于底面,AC⊥BC,點D是AB的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | 24+8$\sqrt{2}$+8$\sqrt{5}$ | B. | 20+8$\sqrt{2}$+4$\sqrt{5}$ | C. | 20+8$\sqrt{5}$+4$\sqrt{2}$ | D. | 20+4$\sqrt{2}$+4$\sqrt{5}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com