

| A. | 24+8$\sqrt{2}$+8$\sqrt{5}$ | B. | 20+8$\sqrt{2}$+4$\sqrt{5}$ | C. | 20+8$\sqrt{5}$+4$\sqrt{2}$ | D. | 20+4$\sqrt{2}$+4$\sqrt{5}$ |
分析 由三視圖還原原幾何體,原幾何體是一個以正視圖為底面的四棱錐,側面PAB與底面ABCD垂直,底面ABCD是邊長為4的正方形,側面PAB是等腰三角形,底邊AB上的高為2,側面PAD、PBC是全等的直角三角形,直角邊AD=4,AP=$2\sqrt{2}$,側面PCD是等腰三角形,底邊CD=4,腰PD=PC=2$\sqrt{6}$.然后由三角形面積求解.
解答 解:由三視圖可得原幾何體如圖: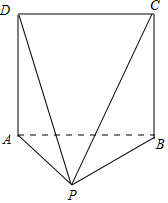
該幾何體是一個以正視圖為底面的四棱錐,
側面PAB與底面ABCD垂直,底面ABCD是邊長為4的正方形;
側面PAB是等腰三角形,底邊AB上的高為2,側面PAD、PBC是全等的直角三角形,直角邊AD=4,AP=$2\sqrt{2}$;
側面PCD是等腰三角形,底邊CD=4,腰PD=PC=2$\sqrt{6}$.
∴幾何體的表面積為:$4×4+\frac{1}{2}×4×2+2×\frac{1}{2}×2\sqrt{2}×4+$$\frac{1}{2}×4×\sqrt{(2\sqrt{6})^{2}-{2}^{2}}$
=20+$8\sqrt{2}$+$4\sqrt{5}$.
故選:B.
點評 本題考查由三視圖求幾何體的表面積,關鍵是由三視圖還原原幾何體,是中檔題.


 小學課時特訓系列答案
小學課時特訓系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(2)>e2f(0),f(2001)>e2001f(0) | B. | f(2)<e2f(0),f(2001)>e2001f(0) | ||
| C. | f(2)>e2f(0),f(2001)<e2001f(0) | D. | f(2)<e2f(0),f(2001)<e2001f(0) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(-3,-\sqrt{6})$ | B. | $(-2,-\sqrt{3})$ | C. | [-2,1) | D. | (-2,1) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
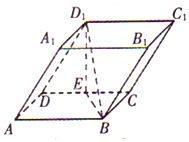 如圖,在四棱柱ABCD-A1B1C1D1中,底面ABCD和側面BCC1B1都是矩形,E是CD的中點,D1E⊥CD,AB=2BC=2.
如圖,在四棱柱ABCD-A1B1C1D1中,底面ABCD和側面BCC1B1都是矩形,E是CD的中點,D1E⊥CD,AB=2BC=2.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com