
分析 x,y是正數,且x,a1,a2,y成等差數列,x,b1,b2,y成等比數列,可得a1+a2=x+y,b1•b2=xy.可得$\frac{{b}_{1}{b}_{2}}{({a}_{1}+{a}_{2})^{2}}$=$\frac{xy}{(x+y)^{2}}$,再利用基本不等式的性質即可得出.
解答 解:∵x,y是正數,且x,a1,a2,y成等差數列,x,b1,b2,y成等比數列,
∴a1+a2=x+y,b1•b2=xy.
則$\frac{{b}_{1}{b}_{2}}{({a}_{1}+{a}_{2})^{2}}$=$\frac{xy}{(x+y)^{2}}$$≤\frac{xy}{4xy}$=$\frac{1}{4}$,當且僅當x=y時取等號.
則$\frac{{b}_{1}{b}_{2}}{({a}_{1}+{a}_{2})^{2}}$的最大值是$\frac{1}{4}$.
故答案為:$\frac{1}{4}$.
點評 本題考查了等差數列與等比數列的通項公式、基本不等式的性質,考查了推理能力與計算能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | (9,10) | B. | (1,9) | C. | (0,9) | D. | (9,11) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
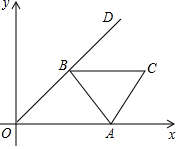 如圖,邊長為3的等邊三角形ABC的頂點A在x軸的正半軸上移動,∠AOD=30°,頂點B在射線,OD上隨之移動,則線段CO的最大值為3$\sqrt{3}$+3.
如圖,邊長為3的等邊三角形ABC的頂點A在x軸的正半軸上移動,∠AOD=30°,頂點B在射線,OD上隨之移動,則線段CO的最大值為3$\sqrt{3}$+3.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
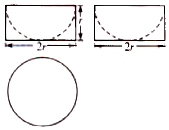 一個幾何體的三視圖如圖所示,其中俯視圖是半徑為r的圓,若該幾何體的體積為9π,則它的表面積是( )
一個幾何體的三視圖如圖所示,其中俯視圖是半徑為r的圓,若該幾何體的體積為9π,則它的表面積是( )| A. | 27π | B. | 36π | C. | 45π | D. | 54π |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com