
分析 (Ⅰ)設出直線AB的方程,聯立直線與拋物線方程,利用數量積為0,求出k,化簡直線方程推出直線必過定點,并求出該定點Q的坐標;
(Ⅱ)利用韋達定理以及弦長公式,表示出三角形的面積,通過換元法,利用函數的單調性求解最小值即可.
解答 解:(Ⅰ)設直線AB的方程為:x=my+t,A($\frac{{{y}_{1}}^{2}}{4}$,y1)、B($\frac{{{y}_{2}}^{2}}{4}$,y2),
聯立$\left\{\begin{array}{l}{{y}^{2}=4x}\\{x=my+t}\end{array}\right.$得y2-4my-4t=0,則y1+y2=4m,與y1y2=-4t,
由$\overrightarrow{OA}•\overrightarrow{OB}=\frac{9}{4}$得:$\frac{({y}_{1}{y}_{2})^{2}}{16}+{y}_{1}{y}_{2}=\frac{9}{4}$⇒y1y2=-18或y1y2=2(舍).
即$-4t=-18⇒t=\frac{9}{2}$,所以直線AB過定點$Q({\frac{9}{2},0})$;
(Ⅱ)由(Ⅰ)得$|{AB}|=\sqrt{1+{m^2}}|{{y_2}-{y_1}}|$=$\sqrt{1+{m^2}}\sqrt{16{m^2}+72}$,
同理得,$|{GD}|=\sqrt{1+{{({-\frac{1}{m}})}^2}}|{{y_2}-{y_1}}|$=$\sqrt{1+\frac{1}{m^2}}\sqrt{\frac{16}{m^2}+72}$,
則四邊形AGBD面積 $S=\frac{1}{2}|{AB}|•|{GD}|=\frac{1}{2}\sqrt{1+{m^2}}$$\sqrt{16{m^2}+72}\sqrt{1+\frac{1}{m^2}}\sqrt{\frac{16}{m^2}+72}$
=$4\sqrt{({2+({{m^2}+\frac{1}{m^2}})})•({85+18({{m^2}+\frac{1}{m^2}})})}$,
令${m^2}+\frac{1}{m^2}=μ({μ≥2})$,
則$S=4\sqrt{18{μ^2}+121μ+170}$是對稱軸為μ<0,開口向上,函數是關于μ的增函數,當μ=2時函數取得最小值.
故Smin=88.
當且僅當m=1時取到最小值88.
點評 本題考查直線與拋物線的位置關系的綜合應用,韋達定理以及弦長公式,函數與方程思想的應用,考查轉化思想以及計算能力.


科目:高中數學 來源: 題型:解答題
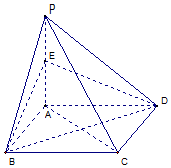 如圖,點P為矩形ABCD所在平面外一點,PA⊥平面ABCD,點E為PA的中點.
如圖,點P為矩形ABCD所在平面外一點,PA⊥平面ABCD,點E為PA的中點.查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
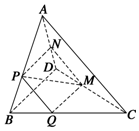 如圖,在四面體ABCD中,截面PQMN是正方形,則下列命題中,正確的為①②④(填序號).
如圖,在四面體ABCD中,截面PQMN是正方形,則下列命題中,正確的為①②④(填序號).查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
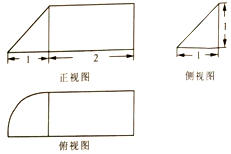
| A. | $\frac{1}{3}+\frac{π}{12}$ | B. | $1+\frac{π}{12}$ | C. | $\frac{1}{3}+\frac{π}{4}$ | D. | $1+\frac{π}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(-ln2,-\frac{1}{3}ln6]$ | B. | $(-\frac{1}{e},-\frac{ln6}{3}]$ | C. | $[\frac{1}{3}ln6,ln2)$ | D. | $[\frac{ln6}{3},\frac{2}{e})$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com