
分析 (1)直接利用求軌跡方程的步驟,由題意列出滿足動點P(x,y)到定點F(1,0)的距離和它到一定直線l:x=4的距離之比為$\frac{1}{2}$的等式,整理后即可得到點P的軌跡;
(2)如果存在滿足條件的定點N,則該點對于m=0的直線也成立,所以先取m=0,與橢圓聯立后解出A、B的坐標,同時求出D、E的坐標,由兩點式寫出AE、BD所在的直線方程,兩直線聯立求出N的坐標,然后證明該點對于m取其它值時也滿足直線AE、BD是相交于定點N,方法是用共線向量基本定理.
解答 解:(1)由題意得$\frac{\sqrt{(x-1)^{2}+{y}^{2}}}{丨x-4丨}$=$\frac{1}{2}$,
即2$\sqrt{(x-1)^{2}+{y}^{2}}$=丨x-4丨,
兩邊平方得:4x2-8x+4+4y2=x2-8x+16.整理得:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
∴動點P(x,y)的軌跡C的方程為橢圓$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
(2)當m變化時,直線AE、BD相交于一定點N($\frac{5}{2}$,0).
證明:如圖,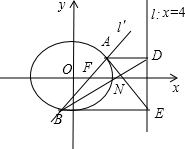
當m=0時,聯立直線x=1與橢圓 $\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,
得A(1,$\frac{3}{2}$)、B(1,-$\frac{3}{2}$)、D(4,$\frac{3}{2}$)、E(4,-$\frac{3}{2}$),
過A、B作直線x=4的垂線,得兩垂足D(4,$\frac{3}{2}$)、E(4,-$\frac{3}{2}$),
由直線方程的兩點式得:直線AE的方程為:2x+2y-5=0,直線BD的方程為:2x-2y-5=0,
方程聯立解得x=$\frac{5}{2}$,y=0,
直線AE、BD相交于一點($\frac{5}{2}$,0).
假設直線AE、BD相交于一定點N($\frac{5}{2}$,0).
證明:設A(my1+1,y1),B(my2+1,y2),則D(4,y1),E(4,y2),
由$\left\{\begin{array}{l}{x=my+1}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,消去x,并整理得(3m2+4)y2+6my-9=0,
△=36m2-4×(3m2+4)×(-9)=144m2+144>0>0,
由韋達定理得y1+y2=-$\frac{6m}{3{m}^{2}+4}$,y1y2=-$\frac{9}{3{m}^{2}+4}$.
由$\overrightarrow{NA}$=(my1-$\frac{3}{2}$,y1),$\overrightarrow{NE}$=($\frac{3}{2}$,y2),
則(my1-$\frac{3}{2}$)y2-$\frac{3}{2}$y1=my1y2-$\frac{3}{2}$(y1+y2)=m×(-$\frac{9}{3{m}^{2}+4}$)-$\frac{3}{2}$×(-$\frac{6m}{3{m}^{2}+4}$)=0
所以,$\overrightarrow{NA}$∥$\overrightarrow{NE}$,所以A、N、E三點共線,
同理可證B、N、D三點共線,所以直線AE、BD相交于一定點N($\frac{5}{2}$,0).
點評 本題考查了軌跡方程,考查了直線與橢圓的綜合,對于定點的存在性問題,先找出滿足條件的特殊點,然后對其它情況進行證明是該類問題常用的方法.屬于中檔題.


 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{π}{12}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
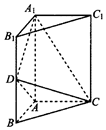 如圖,三棱柱ABC-A1B1C1中,側棱AA1⊥底面ABC,$AB=AC=\frac{1}{2}A{A_1}$,AB⊥AC,D是棱BB1的中點.
如圖,三棱柱ABC-A1B1C1中,側棱AA1⊥底面ABC,$AB=AC=\frac{1}{2}A{A_1}$,AB⊥AC,D是棱BB1的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com