
分析 根據兩點之間的距離公式,表示表示出丨PM丨2,利用換元法及二次函數的性質,即可求得a的值.
解答 解:由丨PM丨2=(2cosθ-a)2+sin2θ=3cos2θ-4acosθ+1+a2,
設cosθ=t,t∈[-1,1],設f(t)=3t2-4at+1+a2,t∈[-1,1],
由二次函數的性質,對稱軸t=$\frac{2a}{3}$,由0<$\frac{2a}{3}$<1時,0<a<$\frac{3}{2}$,
則當t=$\frac{2a}{3}$時,取最小值為:1-$\frac{{a}^{2}}{3}$,則1-$\frac{{a}^{2}}{3}$=$\frac{9}{16}$,解得:a=±$\frac{\sqrt{21}}{4}$,
由0<a<$\frac{3}{2}$,則a=$\frac{\sqrt{21}}{4}$,
當$\frac{2a}{3}$>1時,即a>$\frac{3}{2}$,則f(t)在[-1,1],單調遞減,
則當t=1時取最小值,最小值為:a2+4-4a,
∴a2+4-4a=$\frac{9}{16}$,整理得:16a2-64a+55=0,解得:a=$\frac{11}{4}$或a=$\frac{5}{4}$,
由a>$\frac{3}{2}$,則a=$\frac{11}{4}$,
綜上可知:a的值為:$\frac{\sqrt{21}}{4}$或$\frac{11}{4}$,
故答案為:$\frac{\sqrt{21}}{4}$或$\frac{11}{4}$.
點評 本題考查參數方程的應用,二次函數的性質,考查分類討論思想,屬于中檔題.


 發散思維新課堂系列答案
發散思維新課堂系列答案科目:高中數學 來源: 題型:選擇題
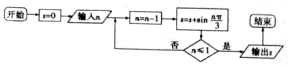
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | 0 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0.2718 | B. | 0.0456 | C. | 0.3174 | D. | 0.1359 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 關于原點對稱 | B. | 關于y軸對稱 | C. | 關于x軸對稱 | D. | 關于直線y=x對稱 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com