Question

6．已知P為函數$y=\frac{4}{x}$的圖象上任一點，過點P作直線PA，PB分別與圓x²+y²=1相切于A，B兩點，直線AB交x軸于M點，交y軸于N點，則△OMN的面積為$\frac{1}{8}$．

Answer 1

分析 設出P（x₀，y₀），得${x}_{0}•{y}_{0}=\frac{1}{4}$．再由圓系方程求出過兩切點A，B的直線方程，分別求出M點，N點的坐標，代入三角形面積公式得答案．

解答 解：設P（x₀，y₀），則${x}_{0}•{y}_{0}=\frac{1}{4}$．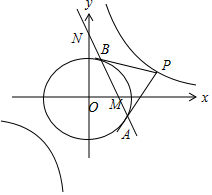
以OP為直徑的圓的方程為$（x-\frac{{x}_{0}}{2}）^{2}+（y-\frac{{y}_{0}}{2}）^{2}=\frac{{{x}_{0}}^{2}+{{y}_{0}}^{2}}{4}$，
整理得：x²+y²-x₀x-y₀y=0，
又圓x²+y²=1，
兩式作差可得x₀x+y₀y=1，即過A、B兩切點的直線方程．
取y=0，得$x=\frac{1}{{x}_{0}}$，取x=0，得y=$\frac{1}{{y}_{0}}$．
∴${S}_{△OMN}=\frac{1}{2}|\frac{1}{{x}_{0}}||\frac{1}{{y}_{0}}|=\frac{1}{2}×\frac{1}{4}=\frac{1}{8}$．
故答案為：$\frac{1}{8}$．

點評 本題考查直線與圓位置關系的應用，考查數學轉化思想方法和數形結合的解題思想方法，求出AB方程是關鍵，是中檔題．