
| A. | $\frac{π}{12}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{12}$ |
分析 根據y=sin(2x+φ)(|φ|<$\frac{π}{2}$)的一條對稱軸方程為x=$\frac{π}{6}$,求出φ.曲線C向左平移θ個單位長度,求出解析式,對稱中心為($\frac{π}{6}$,0),可得θ的值,根據k的不同,即可求出|φ-θ|的最小值.
解答 解::y=sin(2x+φ)(|φ|<$\frac{π}{2}$)的一條對稱軸方程為x=$\frac{π}{6}$,
∴sin($\frac{π}{3}$+φ)=±1,
則$\frac{π}{3}$+φ=$\frac{π}{2}+kπ$,k∈Z.
∵|φ|<$\frac{π}{2}$,
∴φ=$\frac{π}{6}$.
可得y=sin(2x+$\frac{π}{6}$)⇒向左平移θ個單位長度,得:sin(2x+2θ+$\frac{π}{6}$),
對稱中心為($\frac{π}{6}$,0),
則:2×$\frac{π}{6}$+2θ+$\frac{π}{6}$=kπ,k∈Z.
∴θ=$\frac{1}{2}kπ-\frac{π}{4}$.
則|φ-θ|=θ=|$\frac{1}{2}kπ-\frac{π}{4}$-$\frac{π}{6}$|的最小值為:$\frac{π}{12}$.
故選:A.
點評 本題考查了三角函數的性質的運用,屬于基礎題.


 名題訓練系列答案
名題訓練系列答案 期末集結號系列答案
期末集結號系列答案科目:高中數學 來源: 題型:選擇題
| A. | 0.2718 | B. | 0.0456 | C. | 0.3174 | D. | 0.1359 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
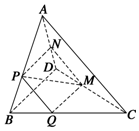 如圖,在四面體ABCD中,截面PQMN是正方形,則下列命題中,正確的為①②④(填序號).
如圖,在四面體ABCD中,截面PQMN是正方形,則下列命題中,正確的為①②④(填序號).查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
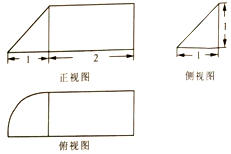
| A. | $\frac{1}{3}+\frac{π}{12}$ | B. | $1+\frac{π}{12}$ | C. | $\frac{1}{3}+\frac{π}{4}$ | D. | $1+\frac{π}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 關于原點對稱 | B. | 關于y軸對稱 | C. | 關于x軸對稱 | D. | 關于直線y=x對稱 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com