
分析 (1)正整數列{an},{bn}滿足:a1≥b1,且對一切k≥2,k∈N*,ak是ak-1與bk-1的等差中項,bk是ak-1與bk-1的等比中項.可得2ak=ak-1+bk-1,bk2=ak-1bk-1,對k取值即可得出.
(2){an}是等差數列,2ak=ak-1+bk-1,2ak=ak-1+ak+1,可得bk-1=ak+1,bk=ak+2,bk2=ak-1bk-1,ak+22=ak-1ak+1,k=2時,a42=a1a3,(a1+3d)2=a1(a1+2d),可得d=0.即可證明.
(3)對一切k≥2,k∈N*,ak是ak-1與bk-1的等差中項,bk是ak-1與bk-1的等比中項.2an=an-1+bn-1,bn2=an-1bn-1,利用基本不等式的性質可得an=$\frac{{a}_{n-1}+{b}_{n-1}}{2}$$≥\sqrt{{a}_{n-1}{b}_{n-1}}$=$\sqrt{{b}_{n}^{2}}$=bn,cn=|an-bn|=an-bn.可得an+1-bn+1=$\frac{{a}_{n}+{b}_{n}}{2}$-$\sqrt{{a}_{n}{b}_{n}}$=$\frac{1}{2}({a}_{n}+{b}_{n}-2\sqrt{{a}_{n}{b}_{n}})$≤$\frac{1}{2}$(an+bn-2bn)=$\frac{1}{2}({a}_{n}-{b}_{n})$,即${c}_{n+1}≤\frac{1}{2}{c}_{n}$.利用等比數列的求和公式即可得出.
解答 解:(1)正整數列{an},{bn}滿足:a1≥b1,且對一切k≥2,k∈N*,
ak是ak-1與bk-1的等差中項,bk是ak-1與bk-1的等比中項.
∴2ak=ak-1+bk-1,bk2=ak-1bk-1,
a2=2,b2=1,可得4=a1+b1,1=a1b1,
解得a1=2+$\sqrt{3}$,b1=2-$\sqrt{3}$.
(2)證明:{an}是等差數列,2ak=ak-1+bk-1,2ak=ak-1+ak+1,可得bk-1=ak+1,
則bk=ak+2,∵bk2=ak-1bk-1,
∴ak+22=ak-1ak+1,k=2時,a42=a1a3,(a1+3d)2=a1(a1+2d),
6a1d+9d2=2a1d,即d(4a1+9d)=0,正整數列{an},可知d≥0,4a1+9d>0,∴d=0.
∴數列{an}為常數數列.
{an}是等差數列的充要條件是{an}為常數數列.
(3)對一切k≥2,k∈N*,ak是ak-1與bk-1的等差中項,bk是ak-1與bk-1的等比中項.
2an=an-1+bn-1,bn2=an-1bn-1,
∴an=$\frac{{a}_{n-1}+{b}_{n-1}}{2}$$≥\sqrt{{a}_{n-1}{b}_{n-1}}$=$\sqrt{{b}_{n}^{2}}$=bn,
又已知a1≥b1,
∴cn=|an-bn|=an-bn.
∴an+1-bn+1=$\frac{{a}_{n}+{b}_{n}}{2}$-$\sqrt{{a}_{n}{b}_{n}}$=$\frac{1}{2}({a}_{n}+{b}_{n}-2\sqrt{{a}_{n}{b}_{n}})$≤$\frac{1}{2}$(an+bn-2bn)=$\frac{1}{2}({a}_{n}-{b}_{n})$,
即${c}_{n+1}≤\frac{1}{2}{c}_{n}$.
∴${c}_{n}≤\frac{1}{2}{c}_{n-1}$$≤\frac{1}{{2}^{2}}{c}_{n-2}$≤…≤$\frac{1}{{2}^{n-1}}{c}_{1}$,
∴c2+…+cn≤$\frac{1}{2}{c}_{1}+\frac{1}{{2}^{2}}{c}_{1}$+…+$\frac{1}{{2}^{n-1}}{c}_{1}$=$(1-\frac{1}{{2}^{n-1}}){c}_{1}$≤c1.
∴當n≥2(n∈N*)時,c2+…+cn≤c1.
點評 本題考查了等差數列與等比數列的通項公式、基本不等式的性質、數列的單調性,考查了推理能力與計算能力,屬于難題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充分必要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -6 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
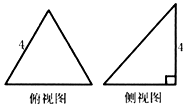 已知三棱錐的俯視圖與側視圖如圖所示,俯視圖是邊長為4的正三角形,側視圖是有一直角邊長為4的直角三角形,則該三棱錐的正視圖可能是( )
已知三棱錐的俯視圖與側視圖如圖所示,俯視圖是邊長為4的正三角形,側視圖是有一直角邊長為4的直角三角形,則該三棱錐的正視圖可能是( )| A. | 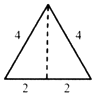 | B. | 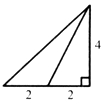 | C. | 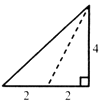 | D. | 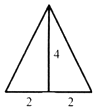 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $(-∞,\frac{{\sqrt{e}}}{e}-8]$ | B. | $[\frac{{\sqrt{e}}}{e}-8,+∞)$ | C. | $[\sqrt{2},e)$ | D. | $(-\frac{{\sqrt{3}}}{3},\frac{e}{2}]$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com