
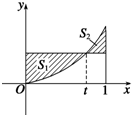
 在區間[0,1]上給定曲線y=x2.試在此區間內確定點t的值,使圖中的陰影部分的面積S1與S2之和最小,并求最小值.
在區間[0,1]上給定曲線y=x2.試在此區間內確定點t的值,使圖中的陰影部分的面積S1與S2之和最小,并求最小值. 分析 先利用定積分分別表示出陰影部分的面積S1與S2,然后求出S1+S2關于t的函數解析式和定義域,利用導數研究函數的單調性,從而求出函數的最小值.
解答 解 S1面積等于邊長為t與t2的矩形面積去掉曲線y=x2與x軸、直線x=t所圍成的面積,即S1=t•t2-?${\;}_{0}^{t}$x2dx=$\frac{2}{3}$t3.
S2的面積等于曲線y=x2與x軸,x=t,x=1圍成的面積去掉矩形面積,矩形邊長分別為t2,1-t,即S2=?${\;}_{t}^{1}$x2dx-t2(1-t)=$\frac{2}{3}$t3-t2+$\frac{1}{3}$.
所以陰影部分面積S=S1+S2=$\frac{4}{3}$t3-t2+$\frac{1}{3}$(0≤t≤1).
令S′(t)=4t2-2t=4t(t-$\frac{1}{2}$)=0時,得t=0或t=$\frac{1}{2}$.
當t=0時,S=$\frac{1}{3}$;
當t=$\frac{1}{2}$時,S=$\frac{1}{4}$;
當t=1時,S=$\frac{2}{3}$.
綜上所述,當t=$\frac{1}{2}$時,S最小,且最小值為$\frac{1}{4}$.
點評 本題主要考查了定積分在求面積中的應用,以及利用導數研究函數的單調性和求函數最值,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | $\frac{x^2}{81}+\frac{y^2}{16}=1$ | B. | x2+y2=1 | C. | $\frac{x^2}{27}+\frac{y^2}{8}=1$ | D. | $\frac{x^2}{3}+\frac{y^2}{2}=1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com